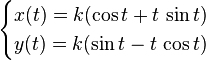Développante du cercle - Définition
La développante du cercle, aussi appelée anti-clothoïde, est une courbe plane développante, c'est-à-dire que ses normales sont les tangentes du cercle.
On en trace souvent sans le savoir : lorsque l'on déroule un fil sous tension d'une bobine circulaire, la main décrit la développante du cercle de la bobine.
Elle fut d'abord étudiée par Huygens lorsqu'il cherchait à concevoir des horloges sans pendule pour une utilisation sur un bateau en mer. Il utilisa la développante du cercle dans une tentative de forcer le pendule à se balancer selon le tracé d'une cycloïde.
Définition mathématique
La courbe peut être définie paramétriquement par l'équation suivante :
On peut également la définir par une équation intrinsèque :
-
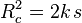
Propriétés et applications
Si on fait rouler sans glisser une droite sur un cercle, chaque point de cette droite décrit, relativement au cercle, une développante de cercle.
On peut aborder la développante de cercle selon une approche cinématique : il s'agit dans ce cas d'une courbe qui, parcourue d’un mouvement uniformément varié, est telle que la vitesse de rotation est constante. On comprend alors le nom d'anti-clothoïde, puisque la clothoïde, elle, est la courbe qui, parcourue d’un mouvement uniforme, est telle que la vitesse de rotation est linéaire.
Les dents des engrenages droits ont un profil en segment de développantes de cercle : cela assure un rapport de vitesse constant et une transmission d'énergie optimum entre les engrenages, puisqu'au point de contact entre deux dents, la tangente au profil est commune aux deux dents. Parmi les autres propriétés remarquables des engrenages à développante, on peut citer les suivantes :
- Si une dent d'engrenage à développante entre en action avec une dent conjuguée du même profil, en rotation à taux uniforme, le mouvement angulaire de la roue menée est aussi uniforme, même quand on fait varier l'entraxe.
- Le taux de mouvement relatif entre la roue menée et la roue menante d'un engrenage à développante est établi par les diamètres de leurs cercles de base.
- Le contact entre les dents conjuguées à développante sur des roues menées et menantes se produit le long d'une droite tangente aux cercles de base de ces roues. C'est ce qu'on appelle la ligne d'action.
- L'usure des surfaces actives est plus régulièrement répartie.
- Les vibrations sont plus faibles qu'avec un autre profil.