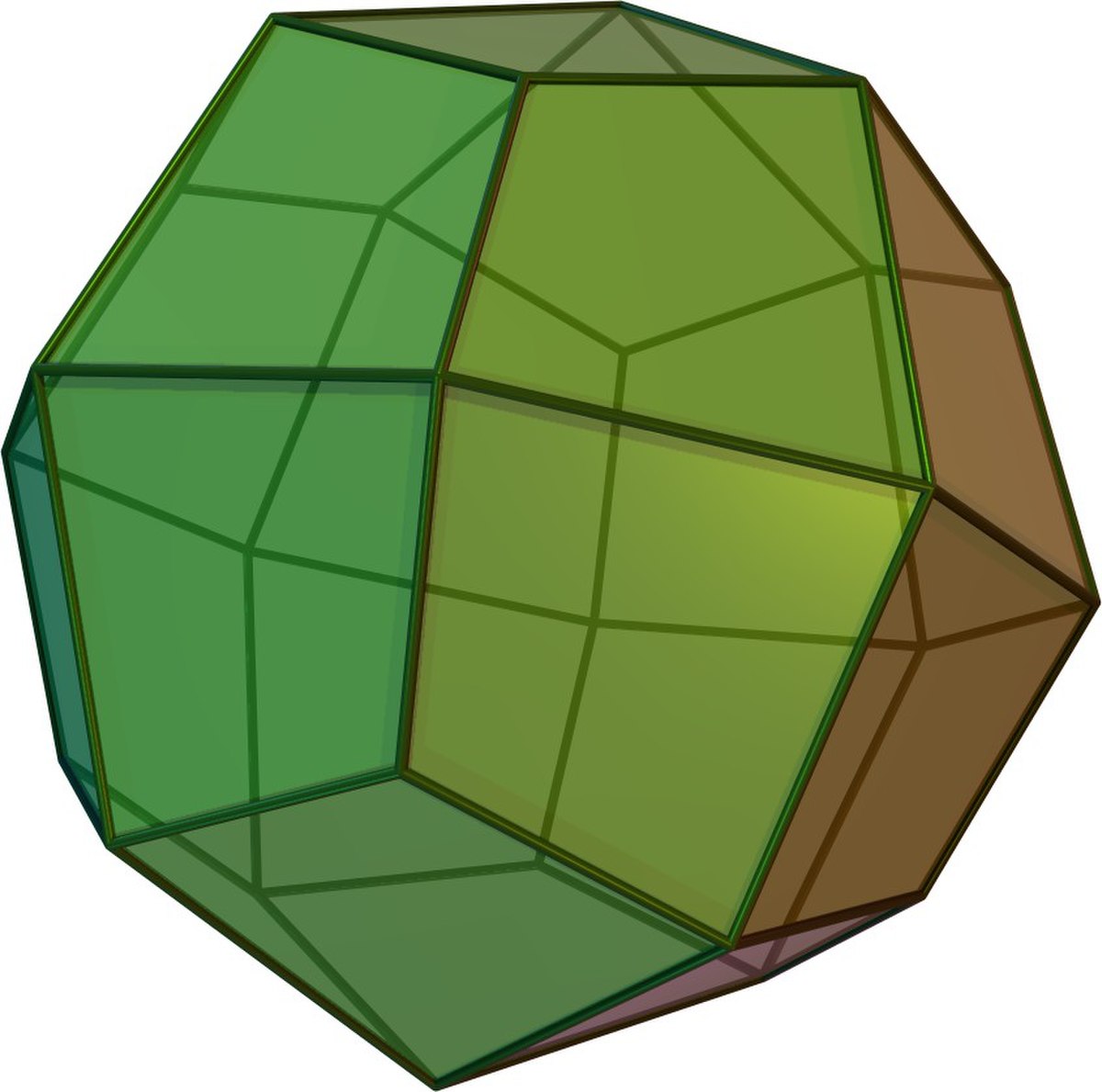
Polytope - Définition
En géométrie, un polytope est la généralisation à toutes dimensions de la notion de polygone pour deux dimensions et de polyèdre pour trois dimensions. Ce terme est aussi utilisé pour une large variété de concepts mathématiques reliés entre eux. Par analogie, le terme de carré peut être utilisé pour indiquer une région de forme carrée du plan ou juste sa frontière, ou même la liste de ses sommets et de ses arêtes ainsi que de l'information sur leurs connexions. Le terme de polytope a été inventé par Alicia Boole Stott, la fille du logicien George Boole.
Les polyèdres réguliers étaient un sujet d'étude majeur chez les anciens mathématiciens grecs (principalement Euclide), probablement à cause de leurs qualités esthétiques. De nos jours, les polytopes ont de nombreuses applications dans les domaines de la programmation linéaire ou en infographie notamment.
Une classe importante de polytopes est celle du polytope convexe qui peut être défini comme l'enveloppe convexe d'un nombre fini de points. Le polytope convexe le plus simple que l'on puisse construire est le simplexe constitué de n+1 sommets dans un espace de dimension n.
Les polytopes convexes peuvent également être définis comme l'intersection bornée d'un nombre fini de demi-espaces. L'égalité des deux représentation est prouvée par le Théorème de Minkowski-Weyl.
Pour toute enveloppe convexe dans un espace de dimension n, on peut prendre des sous-ensembles de sommets linéairements indépendants et définir des n-simplexes à partir de ces sommets. En fait, il est toujours possible de décomposer un polytope convexe en simplexes de sorte que leur union soit le polytope original, et que leurs intersections deux à deux soient l'ensemble vide ou un s-simplexe (avec s < n).
Par exemple : dans le plan, un carré (l'enveloppe convexe de ses sommets) est l'union de deux triangles (2-simplexes) dont l'intersection est la diagonale du carré (1-simplexe).