Diophantien - Définition
Le mot diophantien s'applique à tout ce qui concerne les équations polynomiales à coefficients entiers, également appelées équations diophantiennes. Les notions qui suivent ont été développées pour venir à bout du dixième problème de Hilbert. Il s'agit de savoir s'il existe un algorithme général permettant de dire si, oui ou non, il existe une solution à une équation diophantienne. Le théorème de Matiyasevich prouve l'impossibilté de l'existence d'un tel algorithme.
Ensemble diophantien
Un ensemble M inclus dans
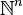
-
- a ∈ M ⇔ il existe x tel que D(a, x) = 0
Ci-dessus, D est un polynôme à coefficients entiers de n+p variables, et x est un paramètre élément de
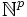
Exemple
- L'ensemble des nombres pairs est diophantien car :
-
- a pair ⇔ il existe x tel que a – 2x = 0
- L'ensemble des nombres non premiers est diophantien car :
-
- a est non premier ⇔ il existe (x,y) tel que a - (x+2)(y+2) = 0
Si M est un ensemble diophantien, inclus dans

-
- a ∈ M ⇔ il existe x, D(a, x) = 0 ⇔ il existe x dans
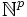

- a ∈ M ⇔ il existe x, D(a, x) = 0 ⇔ il existe x dans
donc M est l'ensemble des valeurs positives d'un polynôme à coefficients entiers, pour des valeurs positives des variables. Par exemple, l'ensemble des nombres de Fibonacci est constitué des valeurs positives du polynôme y(2 – (x2 + xy – y2)2).
Réunion et intersection d'ensembles diophantiens
On montre aisément que la réunion ou l'intersection de deux ensembles diophantiens est diophantien. En effet, si M1 et M2 sont diophantiens, représentés respectivement par les équations D1 et D2, alors :
-
- a ∈ M1 ∪ M2 ⇔ il existe (x,y) tel que D1(a,x)D2(a,y) = 0.
M1 ∪ M2 est donc diophantien, représenté par D(a,x,y) = D1(a,x)D2(a,y).
De même, M1 ∩ M2 est diophantien, représenté par D(a,x,y) = D1(a,x)2 + D2(a,y)2.
Par contre, le complémentaire d'un ensemble diophantien n'est pas toujours diophantien.
Propriété diophantienne
Une propriété P est diophantienne, représentée par l'équation diophantienne D si :
-
- P(a) ⇔ il existe x tel que D(a,x) = 0
Il est équivalent de dire que l'ensemble des a vérifiant la propriété P est un ensemble diophantien. La conjonction ou la disjonction de propriétés diophantiennes est diophantienne. Par contre, la négation ou l'implication ne conserve pas le caractère diophantien.
On définit de proche en proche des propriétés diophantiennes de plus en plus compliquées, par exemple, le fait qu'un entier soit un nombre premier.
Fonction diophantienne
Une fonction F de


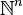
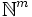
-
- a = F(b) ⇔ il existe x, D(a, b, x) = 0
Les applications polynomiales sont évidemment diophantiennes. Mais on montre également que l'exponentielle est diophantienne, autrement dit, il existe un polynôme D tel que :
-
- a = bn ⇔ il existe x, D(a, b, n, x) = 0
Nous soulignons bien que l'expression de gauche a = bn possède les trois variables a, b et n et est donc une relation exponentielle, et non une simple relation polynomiale telle que a = b3, où n s'est vue fixée la valeur 3. Il est absolument remarquable qu'une expression exponentielle puisse être caractérisée uniquement par des relations polynomiales. Cette propriété, démontrée par Matiyasevich, est un point clé de la réponse négative apportée au 10ème problème de Hilbert. On peut utiliser pour cela le fait que des suites de solutions d'équations diophantiennes peuvent croître exponentiellement. Ainsi, bn est quasiment égal à an où (an) est la suite définie par :
-
- a0 = 0, a1 = 1, an+2 = ban+1 – an
et que :
-
- il existe n, x = an et y = an+1 ⇔ x2 – bxy + y2 = 1
Ou bien, en utilisant un codage passant par l'intermédiaire de solutions d'équations de Pell-Fermat, on montre qu'il y a équivalence entre a = bn et :
-
- il existe (f,g,h,k,l,m,s,t,u,v,w,x,y,z) entiers strictement positifs tels que :
- m2 – (w2 – 1)(w – 1)2z2 = 1
- w = b + h = n + l
- a + g = 2mb – b2 – 1
- (x – y(m – b) – a)2 = (f – 1)2(2mb – b2 – 1)2
- x2 – (m2 – 1)y2 = 1
- u2 – (m2 – 1)v2 = 1
- s2 – (k2 – 1)t2 = 1
- v = ry2
- k = 1 + 4py = m + qu
- s = x + cu
- t = n + 4(d – 1)y
- y = n + e – 1
- il existe (f,g,h,k,l,m,s,t,u,v,w,x,y,z) entiers strictement positifs tels que :
On montre que les coefficients binomiaux sont diophantiens en les considérant comme coefficients dans une base b assez grande de (b+1)n. Il en est de même des factorielles et des nombres premiers.
Le 10ème problème de Hilbert
Le 10ème problème de Hilbert consiste à définir un algorithme acceptant comme paramètre une équation diophantienne D et donnant comme réponse le fait que D admette ou non des solutions. En 1970, Matiyasevic montra qu'il était impossible qu'un tel algorithme existe.
On montre en effet qu'il y a équivalence entre les ensembles diophantiens et les ensembles reconnaissables par machine de Turing (ensembles également dits récursivement énumérables ou semi-calculables). Une machine de Turing modélise un programme donné sur un calculateur universel sans limitation de mémoire. Un ensemble récursivement énumérable E est un ensemble pour lequel il existe un algorithme tel que, si on donne comme paramètre à l'algorithme un élément a de E, alors l'algorithme s'arrête en fournissant une réponse positive, alors que si on donne comme paramètre un élément a n'appartenant pas à E, ou bien l'algorithme s'arrête en donnant une réponse négative, ou bien il boucle indéfiniment. Un ensemble récursivement énumérable est un ensemble dont on peut lister un à un les éléments. On peut être dans l'impossibilité de lister les éléments de son complémentaire.
Tout ensemble diophantien est récursivement énumérable
Il est facile de montrer qu'un ensemble diophantien E défini par une équation D est récursivement énumérable. L'algorithme le reconnaissant est le suivant :
- lire en entrée la valeur du paramètre a
- donner à x la valeur 0
- tant que D(a,x) est différent de 0, augmenter x de 1 fin tant que
Cet algorithme est donné dans le cas où x décrit

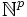

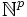
Si a est élément de E, il existera un x tel que D(a,x) = 0. L'algorithme précédent finira par le trouver et s'arrêtera sur cette valeur de x. Par contre, si a n'est pas élément de E, aucun x ne convient, et l'algorithme bouclera indéfiniment. E est donc bien récursivement énumérable.
Tout ensemble récursivement énumérable est diophantien
La réciproque est extrêmement délicate et constitue le nœud du théorème de Matiyasevich. Elle se prouve en codant les configurations d'une machine de Turing par des entiers et en montrant que la fonction qui, à une configuration de la machine au cours du calcul, associe la configuration suivante, est une fonction diophantienne. Si p est un nombre codant une configuration d'une machine de Turing, il existe un polynôme D tel que D(p, x1, ..., xn) possède une solution si et seulement si la Machine de Turing démarrant par la configuration p s'arrête. La reconnaissance des ensembles diophantiens est donc équivalent à celle des ensembles récursivement énumérables.
La méthode précédente permet explicitement d'associer un polynôme à un algorithme définissant un ensemble récursivement énumérable. Ainsi, en 1976, Jones a-t-il explicité un polynôme de degré 25 et des 26 variables a, b, ..., z, dont l'ensemble des valeurs positives coïncide avec l'ensemble des nombres premiers. Le voici :
- (k+2)[1 – (wz+h+j–q)2 – [(gk+2g+k+1)(h+j) + h – z]2
- – (2n+p+q+z–e)2 – [16(k+1)3(k+2)(n+1)2 + 1 – f2]2
- – [e3(e+2)(a+1)2 + 1 – o2]2 – [(a2–1)y2 + 1 – x2]2
- – [16r2y4(a2–1) + 1 – u2]2
- – [((a+u2(u2–a))2–1)(n+4dy)2 + 1 – (x+cu)2]2 – [n+l+v–y]2
- – [(a2–1)l2 + 1 – m2]2 – [ai+k+1–l–i]2
- – [p + l(a–n–1) + b(2an+2a–n2–2n–2) – m]2
- – [q+ y(a–p–1) + s(2ap + 2a – p2 – 2p – 2) – x]2
- – [z + pl(a–p) + t(2ap – p2 – 1) – pm]2]
Impossibilité du 10ème problème de Hilbert
La théorie de la calculabilité a montré qu'il existe des ensembles récursivement énumérables dont le complémentaire n'est pas récursivement énumérable.
Plus précisément, à toute équation diophantienne D sans paramètre, définissons Card(D) comme étant le cardinal de son ensemble de solutions (éventuellement infini). Alors l'ensemble E = {D | Card(D) ≥ 1} est récursivement énumérable. Car si D appartient à un tel ensemble, il suffit d'énumérer les x les uns après les autres et de tester si D(x) est nul pour finir par un trouver un, ce qui permet de dire que D appartient à E. Bien entendu, si D n'admet pas de solution, l'algorithme précédent boucle indéfiniment. Et précisément, on montre que {D | Card(D) = 0} n'est pas récursivement énumérable. Cela signifie qu'il existe bien un algorithme général permettant de dire si une équation diophantienne D admet une solution, mais aucun algorithme permettant de dire si D n'en admet pas.
Le 10ème problème de Hilbert n'admet donc pas de solution. La résolution générale des équations diophantiennes est un problème indécidable.
Bibliographie
Youri Matiiassevitch, Le dixième problème de Hilbert, Masson 1995.

















































