Ensemble flou - Définition

La théorie des ensembles flous est une théorie mathématiques du domaine de l’algèbre abstraite. Elle a été développée par Lotfi Zadeh en 1965 afin de représenter mathématiquement l'imprécision relative à certaines classes d'objets.

Présentation

Les ensembles flous (ou parties floues) ont été introduits afin de modéliser la représentation humaine des connaissances, et ainsi améliorer les performances des systèmes de décision qui utilisent cette modélisation.

Les ensembles flous sont utilisés soit pour modéliser l'incertitude et l'imprécision, soit pour représenter des informations précises sous forme lexicale assimilable par un système expert.

Définition

Les parties floues (ou ensembles flous) sont définies comme des ensembles pouvant contenir des éléments de façon partielle.

Propriétés

• Une partie floue A de B est caractérisée par une application de B dans [0,1]. Cette application, appelée fonction d'appartenance et notée μ_A représente le degré de validité de la proposition " x appartient à A " pour chacun des éléments x de B. Si μ_A(x) = 1, l'objet x appartient totalement à A, et si μ_A(x) = 0, il ne lui appartient pas du tout. Pour un élément x donné, la valeur de la fonction d'appartenance μ_A(x) est appelée degré d'appartenance de l'élément x au sous-ensemble A.

• Le noyau d'une partie floue A est l'ensemble des éléments qui appartiennent totalement à A c'est-à-dire dont le degré d'appartenance à A vaut 1.

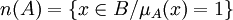
• Le support d'une partie floue A est l'ensemble des éléments appartenant, même très peu, à A c'est-à-dire dont le degré d'appartenance à A est différent de 0.

0 \right\} \," >

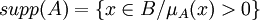
• La hauteur d'un sous-ensemble flou A de E est définie par
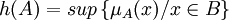
• Une sous-partie floue A de B peut aussi être caractérisée par l'ensemble de ses α-coupes. Une α-coupe d'un ensemble flou A est le sous-ensemble net (classique) des éléments ayant un degré d'appartenance supérieur ou égal à α.

α-coupe(A) = {x B| μ_A(x) ≥ α}

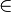
Remarques

La théorie des ensembles flous est très différente de la théorie des ensembles, quoiqu'elle soit basée sur les fondements des mathématiques.

Une différence importante est que, grâce à l'axiome de fondation, un ensemble fini a un nombre fini de sous-ensembles alors qu'il a un nombre infini de sous-ensembles flous.