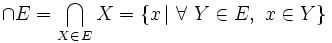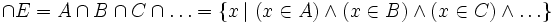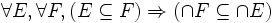Opérations sur les ensembles - Définition
Cet article est consacré à une première approche des opérations sur les ensembles et de leurs propriétés : réunion, intersection, différence, complémentation, différence symétrique...
Réunion
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble U dont les éléments sont ceux de A et de B ( cette proposition, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie axiomatique des ensembles de l'axiome de la paire et de l'axiome de la réunion ). En notation symbolique :
L'unicité de l'ensemble U est garantie par l'axiome d'extensionnalité. On le note " A U B " ( lire " A union B " ), et on l'appelle réunion de A et de B.
Propriétés
- U1 ( commutativité ) : la réunion de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris. En notation symbolique :
- U2 ( Ø élément neutre ) : la réunion de l'ensemble vide avec un ensemble quelconque redonne cet ensemble. En notation symbolique :
- U3 ( idempotence ) : la réunion d'un ensemble quelconque avec lui-même redonne cet ensemble. En notation symbolique :
- U4 : tout ensemble est inclus dans sa réunion avec un autre ensemble. En notation symbolique :
- U5 : un ensemble A est inclus dans un ensemble B si et seulement si leur réunion est égale à B. En notation symbolique :
- U6 : si la réunion de deux ensembles est vide, alors ils sont vides tous les deux. En notation symbolique :
- U7 ( compatibilité avec l'inclusion ) : la réunion de deux sous-ensembles est incluse dans la réunion des deux ensembles dont ils sont sous-ensembles. En notation symbolique :
- U8 ( associativité ) : le résultat de la réunion de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations de réunion sont faites. En notation symbolique :
Ensemble somme
Définition
Pour tout ensemble E dont les éléments sont eux-mêmes des ensembles, il existe un ensemble S dont les éléments sont ceux des éléments de E ( ceci n'est autre que l'Axiome de la réunion ). En notation symbolique :
L'unicité de l'ensemble S est garantie par l'axiome d'extensionnalité. On le note " UE " ( lire " union E " ), parfois " U(E) ", et on l'appelle ensemble somme de E :
Si E = { A, B, C, ... }, alors :
Propriétés
- L'ensemble somme de l'ensemble vide est l'ensemble vide :
- Si E est un sous-ensemble de F, alors l'ensemble somme de E est inclus dans celui de F :
- L'ensemble somme de la réunion de deux ensembles est égal à la réunion des ensembles somme de chaque ensemble :
- Plus généralement, l'ensemble somme de l'ensemble somme d'un ensemble E est égal à la réunion des ensembles somme des éléments de E ; en d'autres termes, si E = { A, B, C, ... }, alors :
Cas des familles d'ensembles
Il est possible de définir la réunion d'une famille quelconque d'ensembles
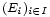
-
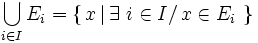
- En particulier, pour une famille vide d'ensembles :
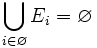
Recouvrements
Un ensemble F est un recouvrement d'un ensemble E si et seulement si l'ensemble somme de F est égal à E. Par exemple, le singleton { E } et l'ensemble des parties
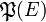
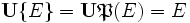
Intersection
Définition
Pour tout ensemble A et tout ensemble B, il existe un ensemble S dont les éléments sont ceux qui sont communs à A et à B. Cette proposition, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie axiomatique des ensembles, du schéma d'axiomes de compréhension. En notation symbolique :
L'unicité de l'ensemble S est garantie par l'axiome d'extensionnalité. On le note " A ∩ B " ( lire " A inter B " ), et on l'appelle intersection de A et de B.
Propriétés
- N1 ( commutativité ) : l'intersection de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris. En notation symbolique :
- N2 ( Ø élément absorbant ) : l'intersection de l'ensemble vide et d'un ensemble quelconque est vide. En notation symbolique :
- N3 ( idempotence ) : l'intersection d'un ensemble quelconque avec lui-même redonne cet ensemble. En notation symbolique :
- N4 : l'intersection de deux ensembles est incluse dans chacun de ces deux ensembles. En notation symbolique :
- N5 : un ensemble A est inclus dans un ensemble B si et seulement si leur intersection est égale à A. En notation symbolique :
- N6 : l'équivalent de U6 se traduit par une définition, celle des ensembles disjoints ( voir ci-dessous ).
- N7 ( compatibilité avec l'inclusion ) : l'intersection de deux sous-ensembles est incluse dans l'intersection des deux ensembles dont ils sont sous-ensembles. En notation symbolique :
- N8 ( associativité ) : le résultat de l'intersection de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations sont faites. En notation symbolique :
Ensemble noyau
Définition
Pour tout ensemble E dont les éléments sont eux-mêmes des ensembles, il existe un ensemble S dont les éléments sont ceux communs à tous les éléments de E ( cette propostion, qui est un axiome implicite de la théorie naïve des ensembles, découle, dans la théorie axiomatique des ensembles du Schéma d'axiomes de compréhension ). En notation symbolique :
L'unicité de l'ensemble S est garantie par l'axiome d'extensionnalité. On le note " ∩E " ( lire " inter E " ), parfois " ∩(E) ", et on l'appelle ensemble noyau ou fonds commun de E :
Si E = { A, B, C, ... }, alors :
Propriétés
- L'ensemble noyau de l'ensemble vide est l'univers Ω des ensembles en entier :
-
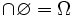
- remarque : selon la théorie des ensembles considérée, l'univers des ensembles peut ne pas exister, mais dans tous les cas, ce n'est pas un ensemble.
- Si E est un sous-ensemble de F, alors l'ensemble noyau de F est inclus dans celui de E :
Cas des familles d'ensembles
Il est possible de définir l'intersection d'une famille quelconque d'ensembles
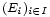
-
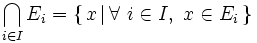
En particulier, pour une famille vide d'ensembles,
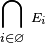
Ensembles disjoints
Deux ensembles sont disjoints si et seulement si leur intersection est vide, c'est-à-dire s'ils n'ont pas d'éléments en commun. Par exemple, si A = { 1, 2 } et B = { 3, 4 }, alors A ∩B = Ø, et A et B sont donc disjoints.
Il existe deux manières de généraliser cette définition à plus de deux ensembles :
- les éléments d'un ensemble E sont (globalement) disjoints si et seulement si l'ensemble noyau de E est vide :
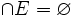
- les éléments d'un ensemble E sont mutuellement disjoints ou disjoints deux à deux si et seulement si l'ensemble noyau de toute paire de ces éléments est vide, c'est-à-dire si :
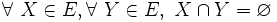
Ces deux notions sont différentes : si des ensembles disjoints deux à deux sont globalement disjoints, des ensembles globalement disjoints ne le sont pas nécessairement deux à deux.
![\forall\ A , \forall\ B , \exists\ U / \, \forall\ X ,\ ( X \in U ) \Leftrightarrow [ ( X \in A ) \vee ( X \in B ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/f/f4b91942247e209a140f7fc6b603c080_8384cfcccc682e9f7c8da2e2d68019b2.png)
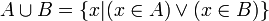
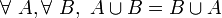
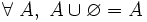
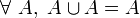
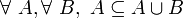
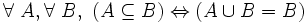
![\forall\ A , \forall\ B ,\ [ A \cup B = \varnothing ] \Rightarrow [ ( A = \varnothing ) \wedge ( B = \varnothing ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/0/0e85f0e5a268ef092d650920fde6f893_4eb44334ca3608e77f26b856675a4f3e.png)
![\forall\ A , \forall\ B , \forall\ C , \forall\ D ,\ [ ( A \subseteq B ) \wedge ( C \subseteq D ) ] \Rightarrow [ ( A \cup C ) \subseteq ( B \cup D ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/5/5fae4c4b501a99d5b4b19536011eb57c_bcf95c6273b82b2ef3cac3c5ac986942.png)
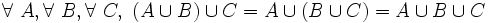
![\forall\ E , \exist\ S /\, \forall\ x ,\ ( x \in S ) \Leftrightarrow [ \ \exist\ A / \, ( A \in E ) \wedge ( x \in A ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c64a3573a70ff608d536c3f49a87b32d_aefc36cd18f2e93c3429b7938f7bbd32.png)
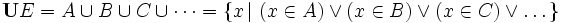
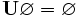
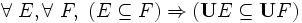
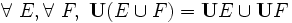
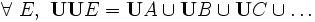
![\forall\ A , \forall\ B , \exist\ S /\, \forall\ X ,\ ( X \in S ) \Leftrightarrow [ ( X \in A ) \wedge ( X \in B ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/1/1dc46410383c9e6e01100abf58c8b870_8ad4f5f18c48610a816207572f2e3f79.png)
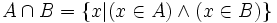
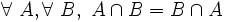
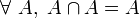
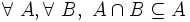
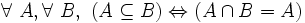
![\forall\ A , \forall\ B , \forall\ C , \forall\ D ,\ [ ( A \subseteq B ) \wedge ( C \subseteq D ) ] \Rightarrow [ ( A \cap C ) \subseteq ( B \cap D ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/e/e03a1eb54cd7c1cc3098a6e415aaac3d_17c52c2ab374d59add78fc2befe53ff2.png)
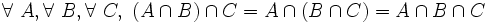
![\forall\ E , \exist\ S /\, \forall\ x ,\ ( x \in S ) \Leftrightarrow [ \ \forall\ A ,\ ( A \in E ) \Rightarrow ( x \in A ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c47d294171539287bcbed0675a7ed757_12420079fe936ff2f9dbfb1a6bad477f.png)