Écoulement de Poiseuille - Définition
Un fluide visqueux, s'il est en écoulement lent dans un tuyau de petit diamètre ou entre deux plaques proches, est en écoulement de Stokes.
En première approximation, si le tuyau est cylindrique ou que les plaques sont parallèles, l'écoulement du fluide est partout parallèle aux parois (approximation de lubrification).
Le frottement aux parois implique qu'aux échelles macroscopiques, la vitesse du fluide y est nulle (condition de non-glissement).
Par ailleurs, la pression ne varie pas dans l'épaisseur de l'écoulement (approximation de lubrification).
Ces trois conditions impliquent que l'écoulement s'organise selon un champ de vitesse parabolique : vitesse nulle aux parois et maximale à mi-hauteur.
Ci-dessous, on considère deux problèmes différents qui donnent lieu à un écoulement de Poiseuille :
- l'écoulement dans un tube de section circulaire et de rayon constant R,
- l'écoulement entre deux plaques planes et parallèles, distantes de h ; ce calcul permet notamment d'évaluer la force entre deux objets (par exemple deux disques) immergés dans un fluide visqueux et s'approchant à une vitesse donnée.
Champ de vitesse dans un tube
La vitesse est parallèle à l'axe du tube (noté z) :
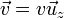
Équation du profil de vitesse :
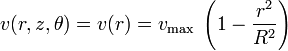
où la vitesse maximale (au centre du tube) est liée au gradient de pression, à la viscosité et au rayon :
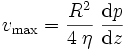
La démonstration de ce résultat est donnée plus bas.
Champ de vitesse entre deux plaques
On suppose que le gradient de pression est orienté selon l'axe x et que la normale aux plaques est orientée selon z, avec les plaques situées en
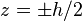
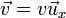
Équation du profil de vitesse :
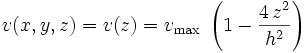
où la vitesse maximale (au centre du tube) est liée au gradient de pression, à la viscosité et à la distance entre les plaques :
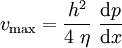
La démonstration de ce résultat est similaire à celle donnée ci-dessous dans le cas du tube circulaire.
Démonstration (dans le cas du tube)
1. Par symétrie, l'écoulement ne varie ni en z, ni en θ :
v(r,z,θ) = v(r)
2. Par conséquent, les seuls efforts de cisaillement sont des forces selon z transmises radialement (selon r) :
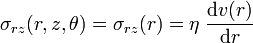
3. Par symétrie également, la variation de la pression est constante le long de l'axe z :
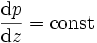
4. Considérons les efforts subis par une zone cylindrique de rayon r et de longueur Δz.
Les efforts de pression sur les deux faces circulaires du cylindre ont une résultante égale à :
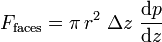
Les contraintes de cisaillement sur le bord du cylindre lui transmettent une force orientée selon son axe z :
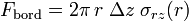
La force totale exercée sur le cylindre de liquide est nulle puisque l'écoulement est permanent. Ainsi :
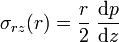
5. Il s'ensuit que le gradient de vitesse est linéaire en r :
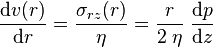
6. Autrement dit, le champ de vitesse est parabolique :
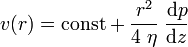
7. Compte tenu de la condition de non-glissement (v(R) = 0) :
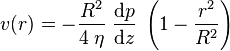
La vitesse est plus importante au centre du conduit malgré le signe négatif, étant donné que la vitesse est orientée à l'encontre du gradient de pression. Écoulement dans le sens positif pour un gradient négatif... CQFD

















































