Dipôle magnétique d'une sphère - Définition

Soit une sphère, de centre O, de rayon R,parcourue par un courant de surface , de moment dipolaire m = k . j₀ V , avec V volume de la boule.

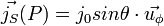
Champ magnétique extérieur

Si r >> R , il est clair que B(M) est celui créé par m .

Très étonnant : c'est vrai pour tout r > R !

Champ magnétique intérieur

Bien sûr , la distribution de courant fait penser à celle d'un solénoïde un peu curieux. Exact !

Le courant s'annule juste sur les bords, de manière que le champ à l'intérieur soit UNIFORME:

B(M) = B(O) = B_externe(0,0,R) par continuité.

Démonstration

La distribution de courant est à support compact : la solution existe et est unique. Il suffit donc de vérifier que la solution donnée satisfait bien à div B = 0 , rot B = 0 et aux conditions aux limites à l'infini ( vrai) et sur la sphère ( [B_ext - B_int]/\ n(P) ) =  : vrai ).

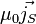
On pourra vérifier que la circulation sur une ligne de champ fermée quelconque satisfait bien le théorème d'Ampère.

Conclusion

Si R devient minuscule, et j0 très grand, m joue le rôle d'une singularité en O , mais B n'y est pas infini, et son intégrale sur la boule vaut ( m) : on prend l'habitude de dire qu'un moment dipolaire par unité de volume J ( en A/m) crée donc le champ d'un dipôle + m.

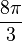
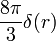
On comparera avec le dipôle électrique d'une boule