Transmission (mécanique) - Définition

La transmission est une des fonctions les plus courantes des éléments de la mécanique générale, c'est-à-dire des dispositifs mécaniques destinés à remplacer la main de l'homme (par opposition à la mécanique, branche de la physique)

Selon les mécanismes, la transmission peut concerner :

• la position
• le mouvement
• la force
• la puissance

Le terme entraînement est aussi employé dans ce sens, notamment dans le cas des mouvements linéaires.

Modes et organes de transmission

Transmission par contact solide

Chaîne de transmission

• Par pression:
  • (arbre dans le cas d'une rotation
  • traction par corde, cordage, sangle ou poussée par tirants
• Par obstacles:
  • transmission par chaîne, courroie synchrone, crémaillère uniquement dans le cas où il s'agit d'éviter tout glissement
  • engrenages
• Par frottement:
  • roue
  • courroie de transmission
  • embrayage

Transmission par fluides

• pneumatique:
  • air comprimé
  • hydraulique (eau) ou (huile)

Transmission sans contact

En utilisant l'électromagnétisme : aimant, électroaimant

Transmission avec des fonctions complémentaires

Dans certains cas, l'environnement impose l'utilisation d'organes spécifiques au sein de la transmission:

• accouplement élastique lorsqu'il s'agit d'absorber des chocs
• joint de Cardan, joint de Oldham pour s'affranchir des mouvements indésirables

Notions liées à la transmission

Rendement d'une transmission de puissance

Dans le cas d'une transmission de puissance, l'objectif est généralement de limiter les pertes. On définit alors le rendement:

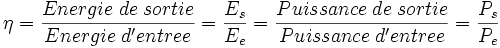
Un engrenage classique a un rendement supérieur à 95% (0,95).

Rapport d'une transmission de vitesse

On définit le rapport de transmission comme étant le rapport des vitesses du mouvement de sortie sur le mouvement d'entrée:

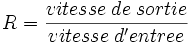
Dans le cas particulier des mouvements d'entrée et sortie de type rotation:

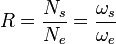
De plus, si on considére la définition des puissances d'entrée et de sortie, à savoir P_e = ω_e.C_e et P_s = ω_s.C_s, où C_e est le couple imposé en entrée, on obtient alors une expression du rapport à partir des efforts transmis:

P_s = η.P_e = ω_s.C_s = η.ω_e.C_e

d'où

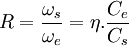
Cela est parfaitement ressenti sur une bicyclette quand on passe un rapport plus court, pour monter une côte par exemple : l'effort à la pédale est moindre, mais la vitesse de rotation du pédalier est plus élevée.