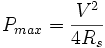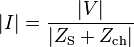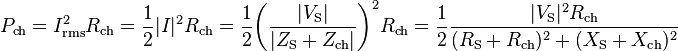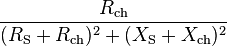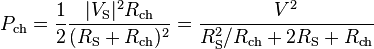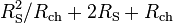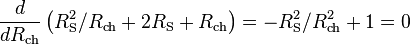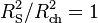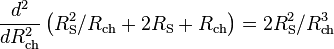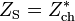Adaptation d'impédances - Définition

Introduction

Est traité ici le sujet concernant les impédances électriques : pour les impédances mécaniques ou motionnelles, voir ces termes.

L’adaptation d'impédances est une technique en électricité permettant d'optimiser le transfert d'une puissance électrique entre un émetteur (source) et un récepteur électrique (charge) :

• Dans le cas de quadripôles en cascade, l'impédance du récepteur doit être très grande par rapport à celle de l'émetteur. Le rendement est ainsi optimisé lors qu'on a une désadaptation maximale.
• La théorie de la puissance maximum détermine que l'impédance de la charge doit être le complexe conjugué de l'impédance du générateur.
• En présence d'une ligne de transmission, l'impédance du récepteur doit être égale à l'impédance caractéristique de celle-ci pour éviter les réflexions. (voir plus loin)

Histoire

Le principe de maximisation du transfert de puissance électrique a été évoqué par Moritz von Jacobi en 1837–1839. Ce principe a été à ses débuts mal interprété, en déduisant qu'un moteur électrique alimenté par une batterie ne pourrait être plus efficace que 50 %, car l'énergie perdue dans la batterie serait au moins aussi importante que celle délivrée au moteur. En 1880, cette interprétation est contestée par Edison et son collègue Francis Robin Upton, qui réalisent que le rendement maximal est différent du transfert de puissance maximale. Pour atteindre le rendement maximal, la résistance de la source (batterie ou dynamo) devrait être minimale. Avec ce constat, ils obtiennent une efficacité de 90 %, et prouvent que le moteur électrique peut être une alternative aux machines thermiques.

L'adaptation d'impédance des lignes de transmission est quant à elle issue de l'industrie téléphonique, pour réduire les échos dans les fréquences audibles. La compagnie Bell semble avoir été à l'origine des études d'adaptation d'impédance. L'autotransformateur à impédance adaptée a été inventé par Emil Berliner et breveté le 4 juin 1877 en tant que système Bell-Berliner.

Les travaux de Oliver Heaviside, mis en application par Mihajlo Pupin vers 1896, sur l'utilisation de bobines de charge pour adapter les longues lignes de transmission ont réellement lancé les études sur les adaptations d'impédance.

Optimisation du transfert d'énergie (Théorie de la puissance maximale)

Source de puissance à gauche et charge à droite.

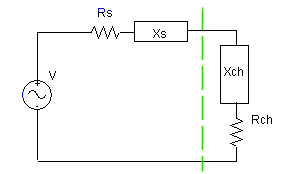
Pour maximiser la puissance transférée il faut adapter les impédances. Pour réaliser cette adaptation, on commence par compenser la partie réactive de l'impédance de la source. Il faut, pour cela que :

.

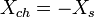
Puis, il faut que la partie résistive de l'impédance de la charge soit égale à la partie résistive de l'impédance de la source :

.

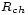
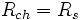
En langage mathématique, les deux impédances sont conjuguées. Dans ce cas, la puissance dissipée dans la résistance de charge est :

Il faut remarquer que la même puissance est alors dissipée dans la résistance de la source.

En vert : puissance transférée à la charge Pch/Pmax.
En rouge : rendement η du système

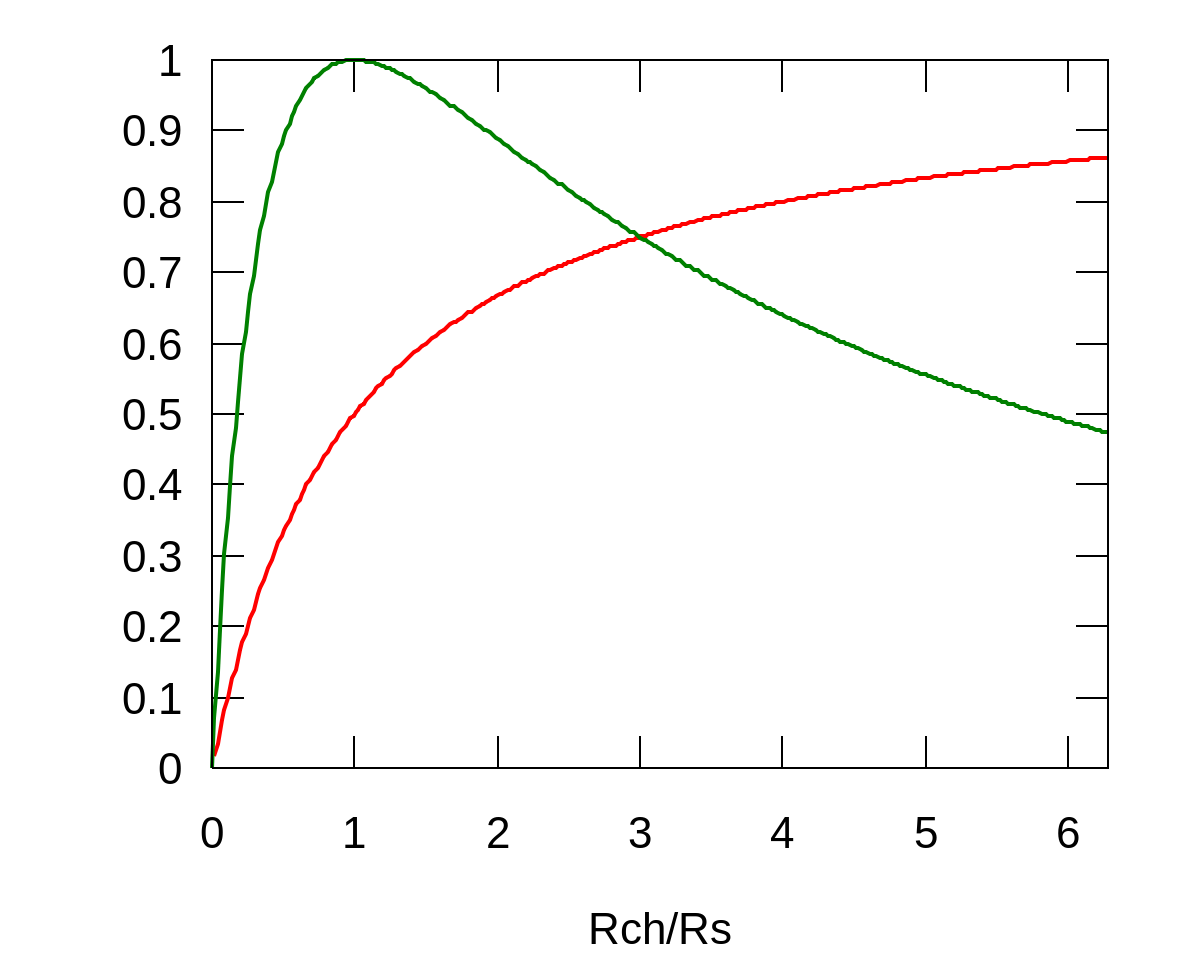
Dans la figure de droite nous avons représenté la puissance relative transférée à la charge en fonction de la résistance de charge. Notez que les deux grandeurs sont exprimées de façon relative. La puissance par rapport à la puissance maximale et la résistance de charge par rapport à la résistance de la source.

Remarquez que le maximum n'est pas très critique. Quand les résistances sont désadaptées d'un facteur 2, la puissance transférée est encore à 89 % du maximum possible.