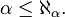Aleph (nombre) - Définition

Aleph-zéro

Aleph-zéro (ℵ₀) est, par définition le cardinal de l'ensemble des entiers naturels. Si l'axiome du choix est vérifié, il s'agit également du plus petit cardinal infini. Un ensemble de cardinal ℵ₀ est un ensemble infini et dénombrable.

Ordinal de Hartogs

Il est possible d'associer à tout ensemble un ordinal initial, que l'on appelle ordinal ou cardinal de Hartogs, de la façon suivante. L'ordinal de Hartogs d'un ensemble a est l'ensemble de tous les ordinaux subpotents à a. Cet ensemble est évidemment un segment initial de la classe des ordinaux, donc un ordinal. Il est également évidemment initial.

Quand a est un ordinal initial ρ, l'ordinal de Hartogs de ρ n'est autre que ρ⁺, le successeur cardinal de ρ.

Continu

Le cardinal de l'ensemble des nombres réels est . Dans le cadre de la théorie des ensembles de Zermelo-Fraenkel munie de l'axiome du choix, l'hypothèse du continu est l'affirmation que  ; en l'absence de cette hypothèse, la place de dans la hiérarchie des aleph n'est pas définie avec certitude, et on peut même démontrer que est compatible avec ZFC pour la plupart des valeurs de α > 0 (mais pas pour α de cofinalité ω, à cause du théorème de König).

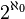
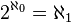
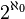
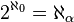
Aleph-un

Aleph-un ( ) est le cardinal de l'ensemble des nombres ordinaux dénombrables (un ensemble lui-même non dénombrable). Si l'axiome du choix est utilisé, est le plus petit cardinal qui suit .

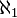
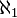
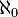
Points fixes

Pour tout ordinal α :

Dans beaucoup de cas, est strictement supérieur à α. Certains ordinaux limites sont des points fixes de la fonction aleph. Le premier cardinal de ce type est la limite de la suite

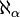
Tout cardinal inaccessible est également un point fixe de la fonction aleph.

Aleph-ω

Le plus petit ordinal infini est noté ω. les ordinaux strictement inférieurs à ω sont les entiers naturels. Le cardinal ℵ_ω est donc par définition la borne supérieure des ℵ_n pour n entier naturel.