Algèbre de Kleene - Définition

Exemples

Soient Σ un ensemble fini (un « alphabet ») et A l'ensemble des expressions rationnelles sur Σ. Deux expressions rationnelles sont égales si elles décrivent le même langage rationnel. L'ensemble A forme une algèbre de Kleene. En fait, il s'agit même d'une algèbre libre de Kleene dans le sens où toute équation valide dans cette algèbre est valide dans toute algèbre de Kleene.

Soit Σ un alphabet. Soit A l'ensemble des langages rationnels sur Σ (ou bien l'ensemble des langages sans contextes sur Σ, ou bien encore l'ensemble de tous les langages récursifs, ou bien enfin l'ensemble de tous les langages sur Σ). L'union (écrite +) et la concaténation (écrite •) de deux éléments de A appartiennent à A, et ainsi l'opération de fermeture de Kleene est un endomorphisme de A. On obtient alors un algèbre de Kleene où : et 1 = {ε}, parfois noté Δ, avec ε qui désigne la chaîne vide, ou mot vide.

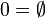
Soit M un monoïde avec comme identité un élément e et soit A l'ensemble des sous-ensembles de M. Soient S et T deux sous-ensembles de M, soit S + T l'union de S et T et ST = {chaîne: s dans S et t dans T}. S* est défini comme le sous-monoïde de M généré par S, intuitivement il correspond à {e} ∪ S ∪ SS ∪ SSS ∪ ... A forme alors une algèbre de Kleene avec comme 0, l'ensemble vide et comme 1, le singleton {e}. On peut faire une construction similaire dans toute petite catégorie.

Supposons M un ensemble et A l'ensemble des relations binaires sur M. On peut munir M des trois opérations des algèbres de Kleene, à savoir l'union pour +, la composition pour • et la fermeture réflexive et transitive pour *. Les deux constantes sont pour 0 la relation vide (qui ne relie rien) et pour 1 la relation pleine (qui relie tout). Ainsi équipé, (M, +, •, *; 0, 1) est une algèbre de Kleene.

Toute algèbre de Boole munie des opérations et s'avère être une algèbre de Kleene si l'on identifie à +, à •, que l'on postule a* = 1 pour tout a et que le 0 pour l'algèbre de Kleene est le 0 de l'algèbre de Boole et de même pour 1.

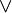
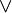
Une algèbre de Kleene spécifique est utile lorsqu'il s'agit de calculer des plus courts chemins dans les graphes orientés pondérés : soit A la droite réelle achevée, posons que a + b est le minimum de a et b et que ab est la somme du réel a et du réel b (la somme de +∞ et -∞ étant par définition +∞). a* est le nombre réel zéro si a est positif ou nul et -∞ si a est strictement négatif. A est une algèbre de Kleene dans laquelle 0 est la valeur +∞ et 1 est le nombre réel zéro.

Histoire

Les algèbres de Kleene n'ont pas été définies par Kleene. Il a introduit les expressions rationnelles et a postulé l'existence d'un ensemble complet d'axiomes qui permettrait de dériver toutes les équations valides dans les expressions rationnelles. Les premiers axiomes ont été proposés par John H. Conway et un système d'axiomes complets définissant les algèbres de Kleene et résolvant le problème a été proposé par Dexter Kozen. qui a démontré leur complétude.