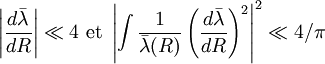Approximation BKW - Définition
La liste des auteurs de cet article est disponible ici.
Démonstration
En faisant apparaître les différents ordres du développement en puissance de

Ordre 0
En n'utilisant que σ0 dans ψ on obtient immédiatement
L'ordre 0, qui s'appelle l'approximation classique, consiste à ne conserver aucun terme en

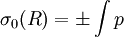
Ordre 1
L'ordre suivant est l'approximation B.K.W. proprement dite.
En reprenant la formule précédente, avec
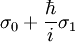

En utilisant la valeur de
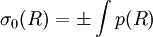
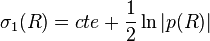
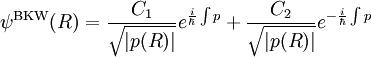
Ordre 2
Le calcul à l'ordre 2 fournit
où
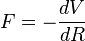
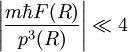
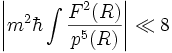
On préfère souvent réécrire ces conditions en utilisant F = pp' / m ce qui amène aux conditions données précédemment qui sont :
Articles liés
- Régime semi-classique
- Théorie des perturbations
États liés
L'une des applications les plus importantes de la théorie BKW concerne le calcul des fonctions d'onde dans un puits de potentiel.
En notant Rint le point tournant classique interne et Rext le point externe et en utilisant les formules de connections en ces deux points on s'aperçoit facilement que la somme des phases des cosinus doit être un multiple de π. On en déduit la condition de quantification, qui est en fait celle trouvée par Niels Bohr et Arnold Sommerfeld en 1913 dans l'ancienne théorie des quanta mais avec le 1/2 en plus
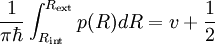
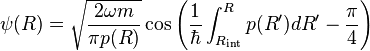
où l'on a normalisé à la fonction d'onde en négligeant la partie classiquement interdite et utilisant l'approximation de l'oscillation rapide du cosinus (
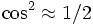
ω désigne la pulsation du mouvement classique et T est la période d'oscillation définies par
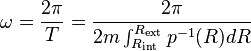
Plus v est grand, plus p l'est, et donc plus l'approximation BKW sera valable (voir la première condition de validité). Il convient tout de même d'être soigneux pour les tout derniers niveaux du potentiel, car l'approximation BKW n'est plus valable (voir la deuxième condition de validité).
Bibliographie
Ouvrages d'introduction pour physicien
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique
- Albert Messiah, Mécanique quantique
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 3 : Mécanique quantique, éd. MIR, Moscou
![\psi(R) = e^{\frac{i}{ \hbar} \left[ \sigma_0 (R) + {\hbar \over i} \sigma_1 (R) + \left(\frac{\hbar}{ i}\right)^2 \sigma_2 (R) + \cdots \right]}](https://static.techno-science.net/illustration/Definitions/autres/0/0dd10a9cb5d3f88e250d903bef808b3d_3f84e1b6472c8ba27531c18b4595b345.png)
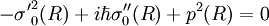
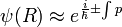
![\psi (R) = {C'_1 \over \sqrt{ |p(R) | } } \left[ 1 - {i m \hbar \over 4} { F(R) \over p^3(R) } - {i m^2 \hbar \over 8} \int { F^2 \over p^5 } \right] e^{ {i \over \hbar} \int p } + {C'_2 \over \sqrt{ |p(R) | } } \left[ 1 + {i m \hbar \over 4} { F(R) \over p^3(R) } + {i m^2 \hbar \over 8} \int { F^2 \over p^5 } \right] e^{- {i \over \hbar} \int p }](https://static.techno-science.net/illustration/Definitions/autres/9/9cbf8c4b5c826c543e61dc842962ba2d_947b56731949d506cbd776f99baccda2.png)