Approximation BKW - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique, l'approximation BKW Brillouin - Kramers - Wentzel est une méthode développée en 1926 qui permet d'étudier le régime semi-classique d'un système quantique. La fonction d'onde est développée asymptotiquement au premier ordre de la puissance du quantum d'action
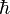
L'idée de base de la méthode BKW est que l'équation de Schrödinger se dérive de l'équation de propagation des ondes. On doit donc retrouver la mécanique classique dans la limite
L'approximation BKW (pour les francophones) est également connue sous les initiales WKB (pour les anglophones), WKBJ, BWKJ et parfois WBK, BWK. Le J supplémentaire est pour le mathématicien Harold Jeffreys, qui a développé en 1923 une méthode générale d'approximation pour des équations différentielles linéaires du second ordre, qui inclut l'équation de Schrödinger à une dimension. Les trois physiciens BKW n'avaient apparemment pas eu connaissance de ce travail.
Formule à une dimension d'espace
De façon générale la fonction d'onde est mise sous la forme ansatz :
![\psi(\vec{r},t) \ = \ A(\vec{r},t) \ \exp \left[ \ \frac{i}{\hbar} \ S(\vec{r},t) \ \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/7e8f7b7f7bacc6a099f9cf9166efbdf1_4e256a7cf098f70da556dde40cee19d2.png)
Les deux fonctions inconnues sont l'amplitude A et l'action S, l'une de ces deux fonctions est en général considérée comme « lentement variable ». En fait seul le cas unidimentionnel où
Formule BKW
Notons ψ la fonction d'onde, solution stationnaire de l'équation de Schrödinger, d'une particule de masse m se déplaçant dans le potentiel V(R) ;
![\left[ -{ \hbar^2 \over 2 m } {d^2 \over d R^2} + V(R) \right] \psi(R) = E \psi(R)](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/3eacd415b13142f61ff90c53311b87c7_1d2c217f52839c31195b2980602bfe46.png)
L'approximation BKW consiste à écrire la fonction d'onde sous la forme
où
Sens physique
Notons le sens physique simple :
- Dans la région classiquement permise plus la particule va vite, plus sa probabilité de présence diminue. En effet là où E > V(R), la probabilité de présence | ψ | 2 sera proportionnelle à
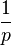
- Dans la région classiquement interdite la probabilité de présence | ψ | 2 sera exponentiellement décroissante en
Domaine de validité
Le domaine de validité de l'approximation est le suivant
-
- Une seconde condition, qui est souvent vérifiée, vient s'ajouter à celle-ci mais elle est rarement utilisée
La première condition peut s'interpréter, en faisant apparaitre le produit
La seconde condition est plus difficile à interpréter mais elle indique qu'il faut être prudent si le potentiel V décroit trop lentement à l'infini.
Cas des points tournants classiques (vitesse nulle)
Les points où p(R) = 0 sont appelés les points de retournements classiques, en effet la vitesse v=p/m y est nulle, le mobile (ou la particule) fera demi-tour. En ces points la première condition n'est plus valable et l'approximation BKW est totalement fausse et il est donc nécessaire d'effectuer un traitement spécial pour ces points.
Au voisinage d'un tel point RC on peut écrire un développement limité du potentiel. En s'arrêtant au premier ordre où
![\psi (R) = C_A {\rm Ai} \left[ \left( R_C- R \right) \left( { 2 m F_C \over \hbar^2} \right)^{1/3} \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/89402175e37d22d45fc086ddff6aa85b_74bd78d6e1e287ed399b287aacce257a.png)
Fonctions de connections
En utilisant les développement asymptotiques de la fonction d'Airy il est possible de les raccorder aux fonctions BKW de part et d'autre d'un point tournant.
Les raccordements de deux fonctions BKW s'en suivent et sont donnés par les lois suivantes.
- La fonction
- La fonction
Signalons qu'il est préférable de ne pas extrapoler d'autres formules car les termes exponentiellement croissant et exponentiellement décroissant ne peuvent en général coexister dans la région classiquement interdite.
Approximation semi-classique uniforme
Notons aussi la formule de l'approximation semi-classique uniforme (ASU) valable dans toutes les régions, donnée par:
![\psi^{\rm ASU} (R) = {C_4 \over \pi} \left[ {3 \hbar^2 \int_{R_C}^R p \over 2 p^3} \right]^{1/6} {\rm Ai}\left[ \left( {3 \int_{R_C}^R p \over 2 \hbar } \right)^{2/3} \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/871a796afbc5e7f840c0e1df51c090c6_28146930061353bd0a3c0fd1d71a64de.png)
