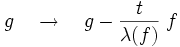Base de Gröbner - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Une façon commode de définir les bases de Gröbner est de faire appel au vocabulaire de la réécriture. C'est l'approche que nous allons adopter ; cependant, l'essentiel des définitions devrait être compréhensible sans connaissance de ces notions.
Règle de réduction
Le point de départ est un procédé de réduction qui, à l'instar de la division euclidienne dans K[X], remplace un polynôme par un autre « plus petit » mais équivalent modulo l'idéal. On appelle monôme un polynôme produit d'indéterminées, et terme un monôme multiplié par un scalaire, son coefficient. Pour définir cette « division euclidienne généralisée », il est utile de choisir une façon d'ordonner les monômes de l'anneau considéré (ce dont on se convainc facilement en essayant de diviser un polynôme de K[X,Y] par un autre).
Un ordre monomial est un ordre total sur les monômes tel que pour tous monômes u, v, w, on ait
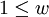
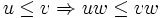
Par exemple, l'ordre lexicographique (lex), équivalent à l'ordre du dictionnaire:  ... quelles que soient les valeurs des puissances (positives) a, b et c. D'autres relations d'ordre sont possibles, pourvu qu'elles vérifient certaines propriétés, destinées à ce que les algorithmes de calculs puissent aller à leur terme, sans boucler par exemple. Les relations d'ordre présentent différentes propriétés et donc certains avantages les unes par rapport aux autres, suivant le type de problème posé. Par exemple, la relation d'ordre "lex", quoique relativement "coûteuse" en temps de calcul, est assez pratique pour faire des projections de la variété associée à l'idéal.
... quelles que soient les valeurs des puissances (positives) a, b et c. D'autres relations d'ordre sont possibles, pourvu qu'elles vérifient certaines propriétés, destinées à ce que les algorithmes de calculs puissent aller à leur terme, sans boucler par exemple. Les relations d'ordre présentent différentes propriétés et donc certains avantages les unes par rapport aux autres, suivant le type de problème posé. Par exemple, la relation d'ordre "lex", quoique relativement "coûteuse" en temps de calcul, est assez pratique pour faire des projections de la variété associée à l'idéal.
Fixons un ordre monomial et une partie finie B de
![K[X_1, \dots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/8/8fb0fc6d41f2ead31891063330737834_c48a4293771ae3962c837de8592de48b.png)
![K[X_1, \dots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/8/8fb0fc6d41f2ead31891063330737834_c48a4293771ae3962c837de8592de48b.png)
si t est le terme de g de plus haut degré divisible par un certain λ(f) avec
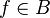
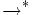

La réduction

Bases de Gröbner
Une base de Gröbner est une partie B pour laquelle la situation est plus favorable.
Soit I un idéal de
![K[X_1, \dots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/8/8fb0fc6d41f2ead31891063330737834_c48a4293771ae3962c837de8592de48b.png)
- La réduction modulo G est confluente (et donc fortement normalisante).
- Un polynôme g appartient à I si et seulement s'il se réduit à 0 modulo G.
- Pour tous f,g de G,
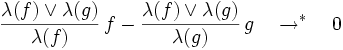
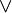
- Les monômes dominants des polynômes de G engendrent le même idéal que les monômes dominants des éléments de I. (Cela implique que G engendre I.)
Cette dernière propriété est la définition usuelle des bases de Gröbner. Elle est pertinente pour leur étude théorique, mais les deux premières formulations sont peut-être plus parlantes. L'assertion 3 fournit quant à elle un moyen simple pour tester si une famille de polynômes est une base de Gröbner.
On peut montrer que tout idéal admet une base de Gröbner. Il n'y a pas unicité : si G est une base de Gröbner de I et si f appartient à I, alors