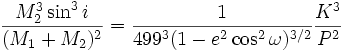Binaire TTL - Définition

Instruments d'observation

• Grands relevés du ciel fournissant des courbes de lumière d'étoiles variables (par ex. les expériences EROS, MACHO, OGLE, DUO, ou bien Hipparcos)

Théorie et application

Equations du mouvement

Si l'on écrit la variation de position de la primaire (objet émetteur) dû à son mouvement orbital autour du barycentre, la différence de temps d'arrivée en seconde s'écrit (Irwin 1952):

avec

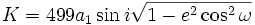
où:

• K = (τ_max-τ_min)/2 = « semi-amplitude » de l'effet de temps de lumière en s.
• a₁ = demi-grand axe de l'orbite de la primaire autour du barycentre en unité astronomique = 1.49597873011×10¹¹m = 499.0047915433 s de temps de lumière.
• e = excentricité de l'orbite.
• ν = anomalie vraie, fonction du temps écoulé depuis la date T du passage au périastre, de la période orbitale, et de l'excentricité.
• ω = angle entre le nœud et le périastre.
• i = inclinaison, angle entre la normale au plan de l'orbite et la ligne de visée.

Fonction de masse

En utilisant la troisième loi de Kepler avec les unités usuelles, le temps de trajet de lumière permet de connaître la fonction de masse définie en masse solaire par :

les variables du membre de gauche étant inconnues tandis que le membre de droite est obtenu par l'analyse de la courbe des O-C en fonction du temps, et où :

• P = période orbitale en année.
• M₁ = masse de la « primaire » en masse solaire. Si la « primaire » est une binaire à éclipse, il s'agit de la somme des masses de ses deux composantes.
• M₂ = masse de la « secondaire » en masse solaire. Si la « primaire » est une binaire à éclipse, il s'agit de la masse du troisième corps.

Paramètres fondamentaux

Pour accéder à la masse du corps perturbateur, il faut soit faire des hypothèses simplificatrices, soit disposer d'informations complémentaires :

• Dans le cas où la primaire est une binaire à éclipses, et donc qu'elle est très vraisemblablement binaire spectroscopique également, la masse totale de cette binaire peut déjà être connue. Pour ce qui est de l'inclinaison, et faute de mieux, on peut faire l'hypothèse que les orbites sont coplanaires pour avoir une estimation de la masse du troisième corps. Sinon on n'a accès qu'à la masse minimale du corps invisible.

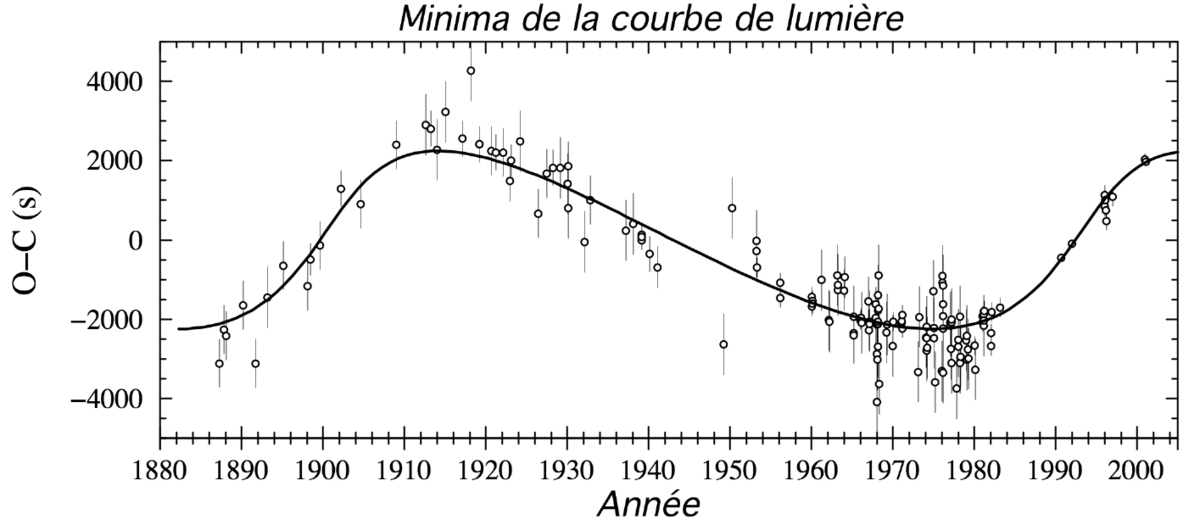
Effet du temps de trajet de lumière pour R Canis Majoris.

• Si l'analyse spectroscopique indique le mouvement orbital, la présence du corps est confirmée et la précision des éléments de l'orbite est améliorée, mais l'inclinaison reste inconnue.
• Par contre, si c'est l'astrométrie qui confirme la duplicité, l'indétermination de l'inclinaison peut être levée. C'est le cas par exemple pour la binaire à éclipses R Canis Majoris, suspectée comme binaire astrométrique à accélération dans le Catalogue Hipparcos ; la combinaison des temps O-C (image ci-contre) et des données astrométriques suggère que le couple primaire de masse 1.24 masse solaire est orbité par un objet de masse 0.34 masse solaire avec une période de 93 ans (Ribas et al. 2002).
• Enfin, l'optimal se produit si l'interférométrie permet de résoudre les composants, car les masses, voire les luminosités, peuvent alors être obtenus. C'est le cas par exemple pour β Cephei (Pigulski & Boratyn 1992).

Détectabilité

• Plus l'objet secondaire est massif, plus il est détectable facilement.
• Pour des masses données, l'effet TTL est proportionnel à P^2/3, rendant plus aisé la détection de binaires à grande période orbitale, et ce, d'autant plus que les mesures de la luminosité d'étoiles variables sont classiquement faites depuis plus d'un siècle.
• L'effet maximum est obtenu quand i=90°, la normale au plan de l'orbite étant perpendiculaire à la ligne de visée.