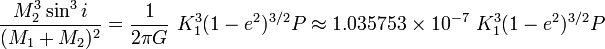Binaire spectroscopique - Définition

Introduction

Mouvement d'une binaire spectroscopique.

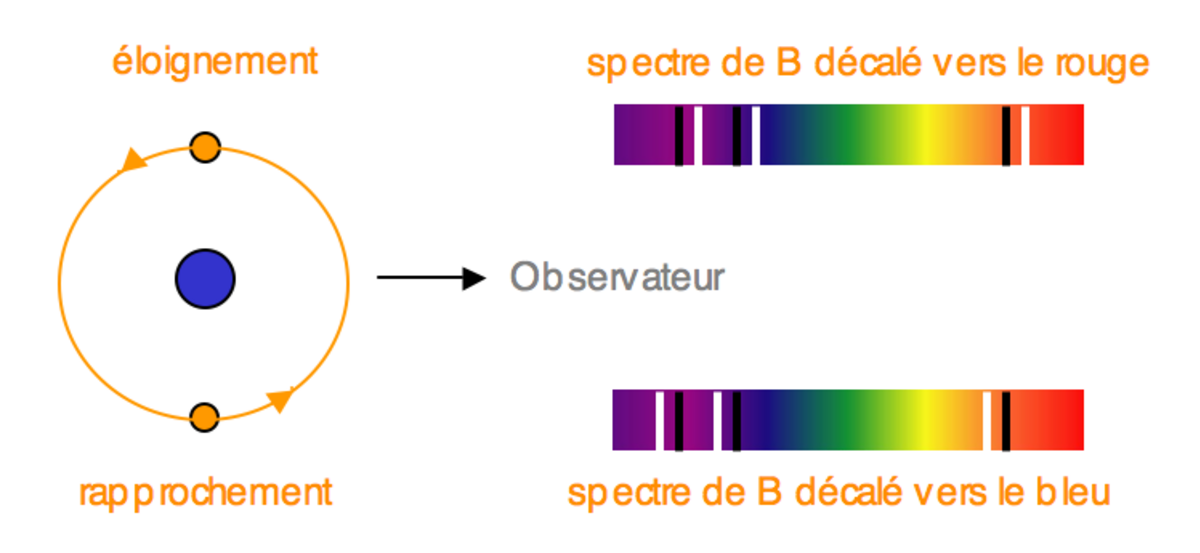
Une binaire spectroscopique est une étoile binaire dont le mouvement orbital est mis en évidence par la variation de la vitesse radiale d'une ou des deux composantes du système. Cette vitesse est mesurée grâce à un spectrographe, en observant le déplacement par effet Doppler-Fizeau des raies spectrales de l'étoile, dû à sa vitesse orbitale le long de la ligne de visée. Cette méthode a également conduit à la détection de la plupart des planètes extrasolaires connues à ce jour.

Historique

Hermann Carl Vogel a été le premier à observer le phénomène oscillatoire des raies d'Algol à l'Observatoire de Potsdam, en novembre 1889 (Vogel, 1890) : avant un minimum de la courbe de lumière de cette binaire à éclipses, l'étoile s'éloignait du Soleil, alors qu'elle s'en rapprochait après ce minimum. Non seulement la duplicité d'Algol était ainsi indépendamment confirmée, mais Vogel donnait également une estimation des diamètres d'Algol et de son « compagnon », ainsi que les masses respectives « 4/9 et 2/9 de masse solaire ». En réalité, Algol est maintenant connue comme un système au moins triple, le couple à éclipses ayant pour masses respectives 3,6 et 0,8 masse solaire.

Courbe des vitesses radiales des deux composantes de la BS2 Mizar A.

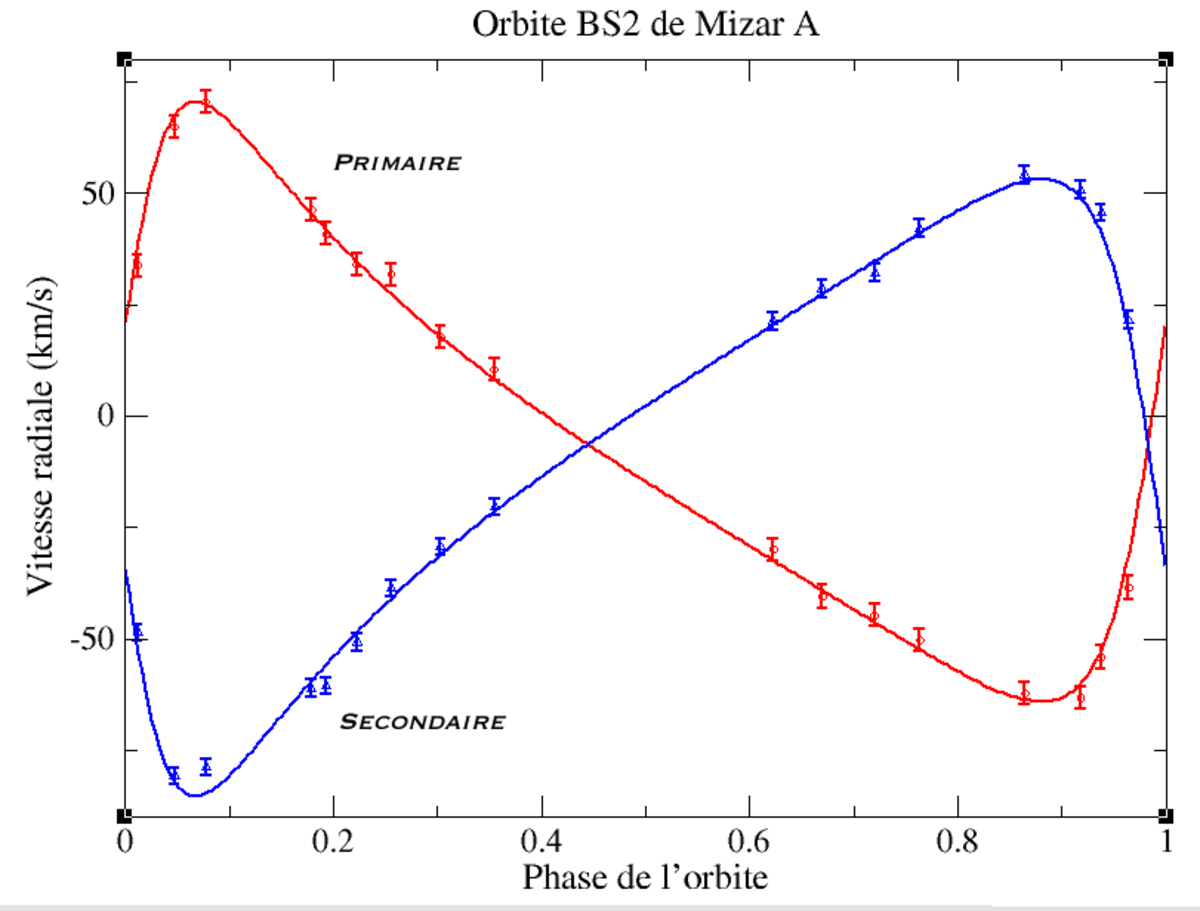
Annoncée simultanément par Edward Charles Pickering le 13 novembre 1889 (Aitken, 1964, indique: août 1889), la première découverte d'une binaire spectroscopique à deux spectres, Mizar, est due à Antonia C. Maury, nièce de Henry Draper, à l'Observatoire d'Harvard (Pickering, 1890). Mizar est en fait une binaire visuelle, dont chacune des composantes, Mizar A et Mizar B sont elles-mêmes des binaires spectroscopiques, ce qui en fait une étoile quadruple. C'est donc en observant Mizar A que Maury s'aperçut que la raie spectrale K du calcium était parfois floue, parfois double, avec une périodicité de 52 jours. L'hypothèse formulée alors fut que Mizar A était « elle-même une étoile double ayant des composantes d'à peu près même luminosité, et trop serrée pour avoir déjà été résolue visuellement. De plus, que la durée de révolution du système est de 104 jours. » (Pickering, 1890). En réalité, la période est de 20,5 jours, l'erreur provenant de l'orbite fortement excentrique et de l'orientation du grand-axe. En 1908, Mizar B fut également découverte comme binaire spectroscopique, mais les raies de la secondaire étaient trop faibles pour être vues.

Le nombre de binaires spectroscopiques connues a depuis régulièrement augmenté. Au 1^er juillet 2003, le 9^ème Catalogue des orbites de binaires spectroscopiques S_B⁹ contenait 1999 orbites concernant 1985 systèmes, contre 1469 systèmes dans le 8^ème Catalogue en 1989.

Les progrès de l'instrumentation, avec des précisions sur les vitesses radiales maintenant meilleures que le m/s, permettent de mesurer des perturbations très petites, dues à des compagnons planétaires et non plus seulement stellaires.

Théorie et application

Equations du mouvement

Dans le cadre d'un simple mouvement Képlerien, chaque composante du système décrit une orbite autour du barycentre. Par dérivation par rapport au temps de la projection de ce mouvement le long de la ligne de visée, z = r sini sin(ν+ω) où r est le rayon vecteur, et en tenant compte également de la vitesse propre du barycentre dans l'espace, on observe pour chaque composante (les indices 1,2 des composantes étant omis) la vitesse radiale:

km/s avec

km/s

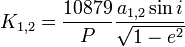
où:

• V_γ = vitesse du barycentre le long de la ligne de visée en km/s.
• K₁ (resp. K₂) = (semi-)amplitude de la courbe de vitesse radiale de la primaire (resp. secondaire) en km/s.
• a₁ (resp. a₂) = demi-grand axe de l'orbite de la primaire (resp. secondaire) autour du barycentre en unité astronomique.
• e = excentricité de l'orbite.
• P = période orbitale en Jour julien.
• ν = anomalie vraie, fonction du temps écoulé depuis la date T du passage au périastre, de la période orbitale, et de l'excentricité.
• ω_1,2 = angle entre le nœud et le périastre. ω₁ est mesuré à partir du nœud ascendant, quand l'étoile s'éloigne de l'observateur et ω₂ = ω₁+π.
• i = inclinaison, angle entre la normale au plan de l'orbite et la ligne de visée.

Fonction de masse

L'intérêt des binaires réside en premier lieu dans la détermination des masses. Si l'on note M₁ (resp. M₂) la masse de l'étoile primaire (resp. secondaire) en masse solaire, on peut maintenant utiliser la troisième loi de Kepler (cf. les binaires astrométriques). On voit alors qu'une binaire spectroscopique donne accès à la fonction de masse définie en masse solaire par :

où les variables du membre de gauche sont inconnues tandis que le membre de droite est obtenu par l'analyse de la courbe de vitesse radiale en fonction du temps t. La période (exprimée en jours) est déterminée souvent grâce à la courbe de lumière qui, repliée en phase φ = (t-T)/P où T est le temps du périastre, apparaît comme périodique. L'amplitude de l'orbite K, exprimée en kilomètres par seconde, est obtenue par mesure des vitesses radiales grâce à l'effet Doppler. La courbe des vitesses radiales, si elle est bien échantillonnée, permet en fait d'obtenir tous les paramètres orbitaux sauf l'inclinaison. À cause de cette limitation, on n'a pas accès directement aux masses individuelles des composantes, car l'inclinaison est (généralement) très difficile à obtenir.

Dans le cas d'une BS2, on a de plus accès au rapport des masses, car M₂/M₁ = K₁/K₂. De même, en inversant la définition de l'amplitude K₁ ci-dessus, il apparaît que le demi-grand axe peut être obtenu dans des unités absolues, et non pas angulaires (dépendantes de la distance) comme c'est le cas avec les orbites astrométriques. Mais, ici encore, c'est à un facteur sin i près.

Paramètres fondamentaux

Pour avoir néanmoins une information concernant les masses de chaque composante, il y a plusieurs méthodes :

• Le cas le plus défavorable se produit quand aucune mesure complémentaire n'est disponible pour une BS1. Comme le type de l'étoile primaire est, au moins grossièrement, connu, une estimation de M₁ est possible. Reste l'inclinaison inconnue qui ne permet de ne connaître que la masse minimum de la secondaire. Statistiquement, on peut utiliser le fait que l'observateur n'a pas une position privilégiée et que toutes les orientations sont équiprobables. On peut montrer alors qu'en moyenne sin i= π/4. Le problème est identique pour une BS2, quoi qu'il soit parfois possible d'obtenir l'inclinaison par polarimétrie.

• La situation s'améliore si la binaire est également connue comme binaire astrométrique, permettant alors de connaître l'inclinaison. Pour une BS2, les masses individuelles sont donc obtenues de manière purement dynamique. Pour une BS1, au contraire, il faut faire une hypothèse sur la masse de la primaire.

• Mieux, si le couple est une également binaire visuelle ou binaire interférométrique: pour une BS2, on acquiert en sus des masses une estimation de la distance indépendante de la parallaxe ainsi que les luminosités. Pour une BS1, les masses sont obtenues si la distance est déjà connue.

• La voie royale concerne les binaires à éclipse (cf. Algol) fournissant alors une estimation de l'inclinaison (voisine de 90 degrés pour qu'une éclipse se produise) obtenue à l'aide d'un modèle. On a alors accès aux masses, luminosités, rayons, températures des étoiles.

Détectabilité

À partir des formules ci-dessus, on peut tirer les conclusions suivantes quant aux capacités de détection des binaires spectroscopiques (ou des planètes extrasolaires) :

• Plus l'objet secondaire est massif, plus il est détectable facilement.
• Pour des masses données, en insérant la 3^ème loi de Kepler dans l'expression de l'amplitude, on a , donc la sensibilité sera meilleure aux courtes périodes orbitales, donc des couples serrés.
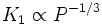
• La vitesse maximale est obtenue quand i=90 degrés, le plan de l'orbite étant parallèle à la ligne de visée.