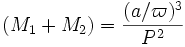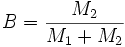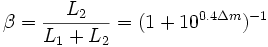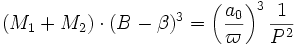Binaire astrométrique - Définition

Introduction

Mouvement de Sirius sur le ciel, d'après Camille Flammarion

Une binaire astrométrique est une étoile binaire dont les deux composantes ne sont pas résolues, la duplicité étant révélée par le mouvement orbital du photocentre sur le ciel. En particulier, quand le compagnon est beaucoup plus faible que l'étoile primaire, c'est le mouvement réflexe de celle-ci qui est observé. Des mesures astrométriques précises et très exactes sont nécessaires pour détecter ces objets, mais cette méthode pourrait conduire dans le futur à la détection de nombreuses planètes extrasolaires.

Historique

Après avoir été le premier à estimer précisément une parallaxe stellaire, celle de 61 Cygni en 1838, Bessel allait également découvrir par hasard les deux premières binaires astrométriques. Dans une lettre du 10 août 1844, Bessel indiquait que le mouvement propre de Sirius et Procyon n'était pas constant. Après avoir éliminé différentes hypothèses, il concluait avec justesse dans les deux cas à la présence d'un corps massif mais obscur orbitant avec une période d'environ un demi-siècle, une hypothèse pourtant perturbante qu'il justifiait par : « La lumière n'est pas une propriété réelle de la masse. L'existence d'innombrables étoiles visibles n'exclut pas l'existence d'innombrables étoiles invisibles ».

Cette découverte n'est pas sans rappeler la prédiction de Neptune par Urbain Le Verrier deux ans plus tard, dont François Arago dit qu'il « vit le nouvel astre au bout de sa plume ». Pour les binaires astrométriques, la confirmation nécessita cependant plus de temps. Il fallut attendre 7 ans pour que l'orbite de Sirius fut effectivement calculée (Peters 1851), le compagnon de Sirius ne fut aperçu qu'en 1862 par Alvan Graham Clark et celui de Procyon qu'en 1896 par John M. Schaeberle, transformant du coup ces binaires astrométriques en binaires visuelles. Ces nouveaux compagnons furent d'ailleurs les premières naines blanches connues.

Ce premier succès ne fut néanmoins pas suivi d'une avalanche de nouveaux résultats. Plus d'un siècle plus tard, on ne dénombrait que 17 binaires astrométriques (et 14 cas suspects) seulement (van de Kamp, 1975).

L'astrométrie demande des observations très exactes, et peut conduire dans le cas contraire à des résultats incorrects. En 1943, K. Strand annonçait la présence d'une planète extrasolaire autour de l'étoile 61 Cygni. En 1960, S. Lippincott faisait une annonce identique pour Lalande 21185. En 1963, P. Van de Kamp trouvait une planète massive d'une période de 24 ans autour de l'étoile de Barnard, puis indiquait en 1978 qu'il s'agissait de deux planètes. Aucune de ces annonces n'a été confirmée depuis et l'explication la plus vraisemblable serait la présence d'erreurs systématiques dans les observations.

Les développements technologiques récents et à venir pourraient néanmoins changer la donne, quantitativement et qualitativement. En particulier, le Catalogue Hipparcos contient environ 4000 objets suspectés d'être des binaires astrométriques.

Théorie et application

Equations du mouvement

Le photocentre décrit une orbite autour du barycentre qui est homothétique en règle générale à celle de l'étoile la plus brillante mais avec un demi-grand axe a₀ pouvant être différent en taille. Les variations de position en coordonnées équatoriales sur le plan tangent du ciel s'écrivent :

où:

• e = excentricité de l'orbite.
• ν = anomalie vraie, fonction du temps écoulé depuis le passage au périastre, de la période orbitale, de la date de passage au périastre et de l'excentricité.
• ω = angle entre le nœud et le périastre.
• Ω = angle de position du nœud ascendant.
• i = inclinaison, angle entre la normale au plan de l'orbite et la ligne de visée.

Fonction de masse

Même si l'on ne voit pas l'orbite de chacune des composantes, ni l'orbite relative de la secondaire autour de la primaire, la troisième loi de Kepler en unités adaptées indique néanmoins que :

où :

• M₁ = masse de l'étoile primaire en masse solaire.
• M₂ = masse de l'objet secondaire en masse solaire.
• a₁ = demi-grand axe de l'orbite de la primaire autour du barycentre en seconde d'arc.
• a₂ = demi-grand axe de l'orbite de la secondaire autour du barycentre en seconde d'arc.
• a = a₁+a₂ = demi-grand axe de l'orbite relative en seconde d'arc.
• = parallaxe annuelle en seconde d'arc
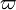
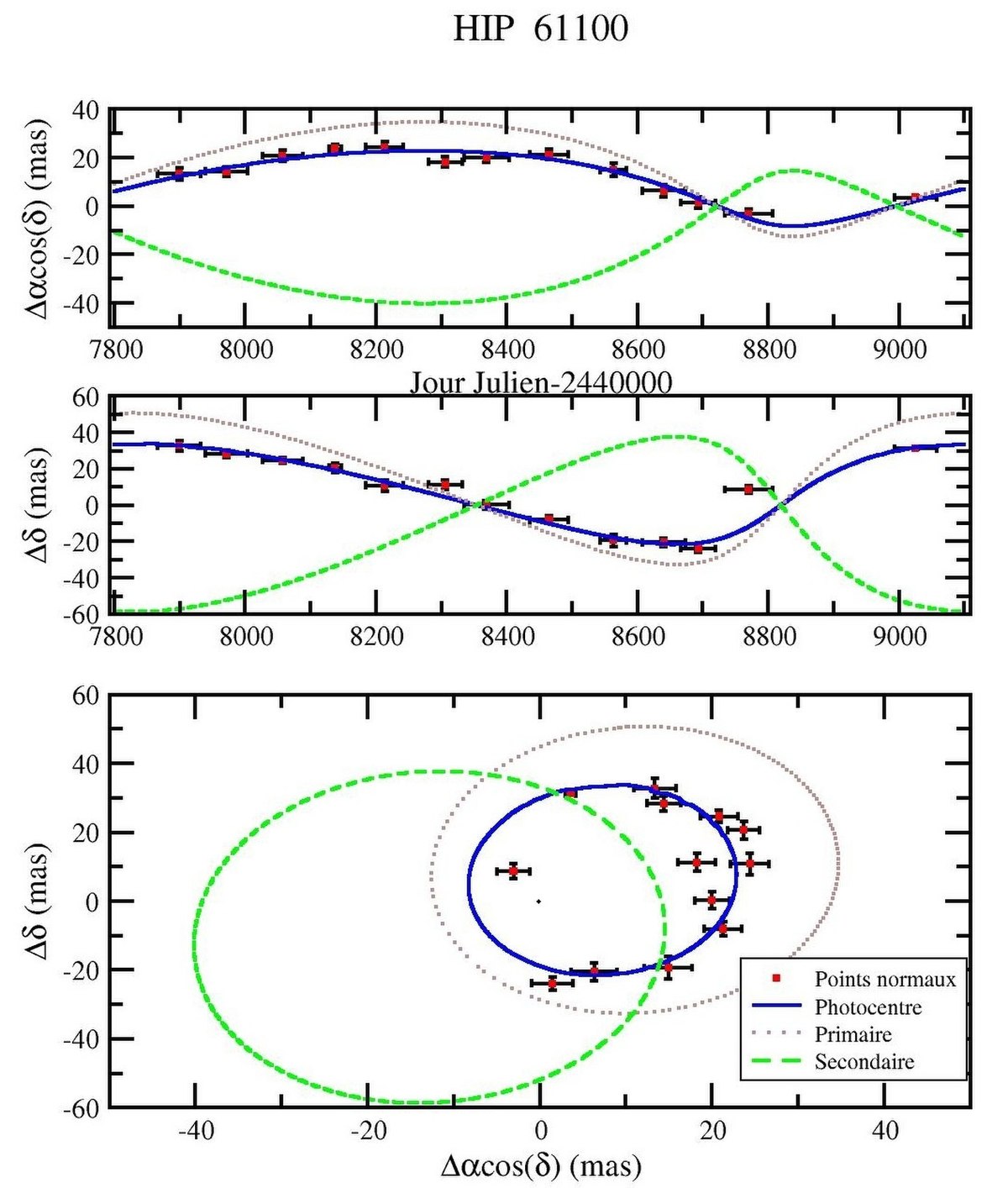
• P = période orbitale en années.

D'autre part, par définition du centre de gravité, on a a₁M₁ = a₂M₂ donc a₁ = Ba où la masse fractionnaire de la secondaire est notée

De même, si l'on note

• L₁ = luminosité de l'étoile primaire en luminosité solaire dans la bande spectrale observée,
• L₂ = luminosité de l'objet secondaire avec les mêmes unités,
• Δm = -2.5 log(L₂/L₁) la différence de magnitude entre les composantes,

alors, la distance d du photocentre à la primaire est telle que dL₁ = (a − d)L₂, soit d = βa où la luminosité fractionnaire est notée

Connaître cette différence de magnitude donnerait accès aux magnitudes de chaque composante, car la magnitude de l'objet non résolu est déjà mesurée. Le demi-grand axe de l'orbite du photocentre vaut donc

a₀ = (B − β)a

En général ce terme est positif, par exemple quand les deux composantes sont sur la séquence principale, mais le signe contraire peut également se produire dans certains cas.

La troisième loi de Kepler montre ainsi qu'une binaire astrométrique permet de donner accès à la fonction de masses (et de luminosités)

où les variables du membre de gauche sont inconnues tandis que le membre de droite est obtenu par l'analyse astrométrique.

Masses et luminosités

On voit qu'une seule équation pour les trois inconnues que sont les masses et la différence de magnitude renseigne peu sur la nature des objets en présence... Pour en savoir plus, il faut soit recourir à des hypothèses supplémentaires, soit être en présence d'une binaire spectroscopique, quand c'est possible.

Mouvement en ascension droite et déclinaison, après soustraction du mouvement propre et du mouvement parallactique, de la binaire astrométrique HIP 61100, également binaire spectroscopique à deux spectres. Les mesures d'Hipparcos ainsi que les orbites de la primaire, de la secondaire, et du photocentre sont indiquées.

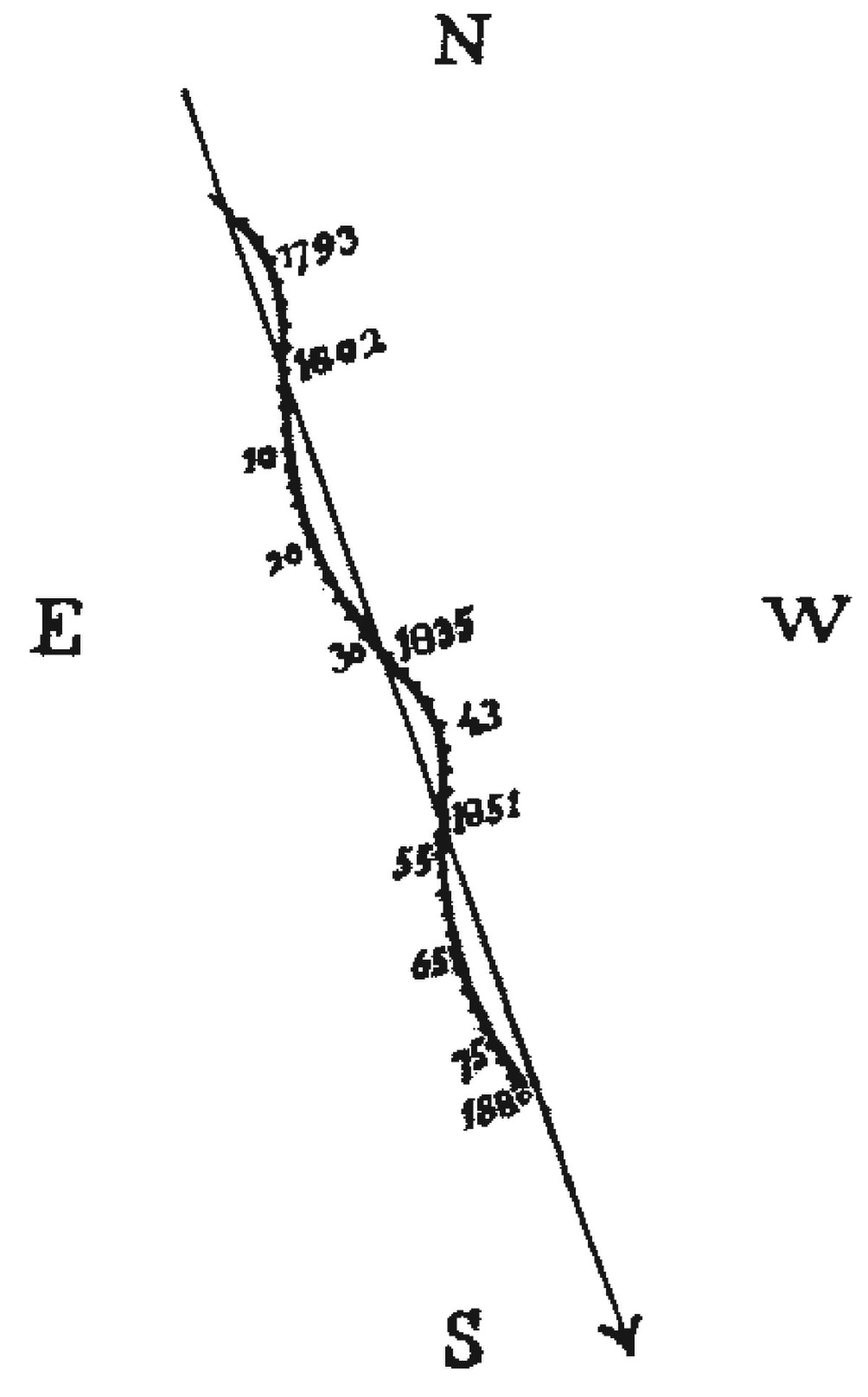
• Le cas le plus favorable se produit quand l'objet peut également être détecté comme binaire spectroscopique à deux spectres (binaire nommée BS2). L'union faisant la force, l'orbite astrométrique lève l'ambiguïté de l'inclinaison qui handicape les orbites spectroscopiques, et les masses de chaque composante sont alors obtenues. La fonction de masses ci-dessus donne alors accès à la différence de magnitude. Les masses et luminosités de chaque composante sont obtenues, comme dans l'exemple illustré ci-contre. Dans cet exemple, l'étoile est détectée comme binaire stochastique par Hipparcos, mais la précision des mesures ne permet pas d'avoir une orbite. Détectée également comme BS2 de période 4,5 ans par le spectromètre Coravel, la combinaison des mesures astrométriques et spectroscopiques indiquerait que M₁ = 0,7, M₂ = 0,6 masse solaire, Δm = 1,8 magnitudes.
• Quand l'objet est connu comme binaire spectroscopique à un spectre seulement (SB1), tout n'est pas perdu. Dans un tel cas, non seulement l'orbite spectroscopique aide à la détermination de l'ensemble des paramètres orbitaux, mais de plus la secondaire peut être considérée comme beaucoup plus faible que la primaire. Par conséquent, on peut considérer que et . La couleur et la magnitude absolue de l'objet non résolu sont donc essentiellement celles de la primaire. À l'aide d'un modèle, on en déduit approximativement la masse de la primaire, et la masse de la secondaire s'en déduit par la fonction de masse ci-dessus. Naturellement, il ne s'agit là que d'une approximation.

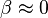
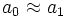
Détectabilité

La détection, la confirmation, la précision de l'orbite dépendent de la grandeur du demi-grand axe de l'orbite du photocentre, ou en tout cas de l'erreur relative sur celui-ci. Compte tenu des relations ci-dessus :

• Elle sera connue d'autant plus précisément que l'objet sera proche (parallaxe grande).
• Pour ce qui concerne les masses et luminosités, on note deux cas extrêmes. Quand , par exemple pour deux objets jumeaux, aucun signal astrométrique ne peut être observé. De même, quand le compagnon secondaire a une très petite masse et une très faible luminosité comparativement à la primaire, et c'est en particulier le cas pour les planètes extrasolaires. Les capacités de détection par l'astrométrie sont optimales quand | B − β | est maximum.
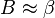
• Pour des masses et luminosités données, , donc la sensibilité sera meilleure aux longues périodes orbitales, pour autant que la base de temps d'observation soit assez longue.
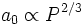
• Enfin, au contraire des binaires visuelles pour lesquelles c'est le mouvement relatif des deux composantes qui est mesuré, la détection des binaires astrométriques nécessite d'avoir un repère de référence très précis pour minimiser les erreurs systématiques, une des raisons expliquant le besoin d'astrométrie spatiale.