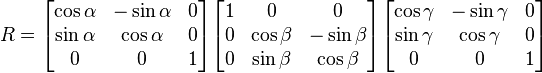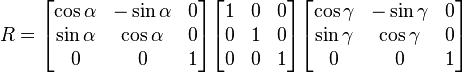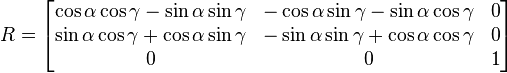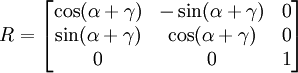Blocage de cardan - Définition

Le blocage de cardan en mathématiques appliquées

Le problème du blocage de cardan apparaît lorsque l'on utilise les angles d'Euler dans une application des mathematiques, par exemple dans un logiciel (modélisation 3D, système de navigation embarqué, jeu vidéo, métavers, ...).

Les angles d'Euler offrent une description numérique d'une rotation quelconque de l'espace à trois dimensions au moyen de trois nombres.

Pour faire une comparaison, toutes les translations peuvent se décrire au moyen de trois nombres x, y et z comme la succession de trois mouvements en ligne droite le long de trois axes perpendiculaires X, Y et Z. Il en va de même pour les rotations, toutes les rotations peuvent se décrire au moyen de trois nombres α, β et γ, comme la succession de trois mouvements de rotation autour de trois axes perpendiculaires l'un avec le suivant. Cette ressemblance entre les coordonnées linéaires et les coordonnées angulaires rend les angles d'Euler très intuitifs, mais malheureusement ils souffrent du problème du blocage de cardan.

Perte d'un degré de liberté avec les angles d'Euler

Une rotation de l'espace à trois dimensions peut se représenter numériquement au moyen de matrices de plusieurs manières. Une de ces représentations est :

avec α et γ contraints dans l'intervalle [ − π,π] et β contraint dans l'intervalle [0,π].

Examinons par exemple ce qui se passe lorsque β = 0. Comme et , l'expression ci-dessus devient égale à :

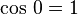
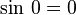
La seconde matrice est la matrice identité et n'a pas d'effet sur le produit. Si l'on multiplie la première matrice par la troisième, on obtient :

Enfin, en appliquant les formules de trigonométrie :

Changer les valeurs de α et de γ dans la matrice ci-dessus a le même effet : l'angle de rotation α + γ change, mais l'axe de rotation reste dans la direction Z. La dernière colonne et la dernière ligne de la matrice ne changeront pas : un degré de liberté a été perdu.

La seule solution pour que α et γ recommencent à jouer des rôles différents est d'éloigner β de la valeur 0.

Un problème semblable apparaît lorsque β = π.

On peut choisir d'autres conventions pour représenter une rotation avec une matrice au moyen d'angles d'Euler que la convention Z-X-Z ci-dessus et on peut également choisir d'autres intervalles de variation pour les angles, mais dans tous les cas, il y a au moins une valeur pour laquelle un degré de liberté est perdu.

On remarquera que le problème du blocage de cardan ne rend pas les angles d'Euler « faux » (ils continuent à jouer leur rôle de système de coordonnées), mais les rend mal adaptés à certaines applications pratiques.

La solution des quaternions

Une autre représentation des rotations dans l'espace à trois dimensions est celle des quaternions.

Un quaternion est un quadruplet qui représente dans le cas général une similitude géometrique. Si la relation s² + x² + y² + z² = 1 est vérifiée, alors le quaternion peut être utilisé pour représenter une rotation.

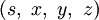
D'un point de vue pratique, une rotation d'angle autour de l'axe dirigé par un vecteur unitaire est représentée par le quaternion .

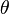
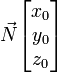
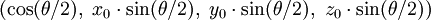
Il n'y a pas de problème équivalent à celui du blocage de cardan avec les quaternions. Cela peut s'expliquer de manière intuitive par le fait qu'un quaternion décrit une rotation en bloc (« veuillez tourner de radians autour de l'axe porté par le vecteur  »), tandis que les angles d'Euler sont composés de trois rotations successives.

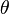
En plus de cela, les quaternions ont d'autres avantages sur les angles d'Euler.