Bulle de savon - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une bulle de savon est un globe formé d'un mince film d'eau savonneuse rempli d'air qui flotte dans l'atmosphère.
Sa paroi est constituée de deux rangées de phospholipides amphiphiles de par leurs "têtes" hydrophiles et leurs "queues" hydrophobes. Une étroite couche d'eau est retenue entre les têtes hydrophiles tandis que les queues hydrophobes, préférant le contact de l'air plutôt que celui de l'eau (comme leur nom l'indique), s'agencent de la manière suivante :
- queues de la rangée phospholipidique externe : tournées vers l'extérieur de la bulle, donc vers l'air ambiant.
- queues de la rangée phospholipidique interne : tournées vers l'intérieur de la bulle, donc vers l'air emprisonné.
La réalisation de bulle de savon, de simple jeu enfantin attesté par la peinture depuis le XVIIIe siècle, est devenu de nos jours un véritable sport, avec ses concours et ses compétitions.
Physique
Étude de la forme d'une bulle de savon
En raison de la tension superficielle, les films d'eau savonneuse sont dotés d'une certaine élasticité et il faut dépenser un peu d'énergie pour les étirer, comme on le fait sans s'en rendre compte lorsque l'on produit une bulle de savon. Ce phénomène peut, dans une certaine mesure, être comparé au gonflage d'un ballon de baudruche, à ceci près que le film d'eau savonneuse est constitué de liquide et que l'énergie mise en jeu pour produire une bulle est beaucoup moins importante. Il reste que la pression du gaz contenu dans une bulle est légèrement plus forte que celle de l'atmosphère environnante.
Plus l'aire d'un film liquide est importante, plus son énergie potentielle est élevée. Or, tout système matériel atteint un équilibre stable lorsque son énergie potentielle est minimale. Une bulle de savon tend donc, naturellement, à prendre la forme qui lui permet d'enfermer un volume d'air donné dans une surface d'aire minimale ; tout le monde a pu constater qu'il s'agit d'une sphère, mais constater n'est pas démontrer et les mathématiciens, Archimède en tête, s'y sont longtemps cassé les dents. Il fallut attendre 1882 pour que le mathématicien allemand Hermann Amandus Schwarz prouve que parmi toutes les surfaces enfermant un volume donné, la sphère est bien celle qui présente l'aire minimale (cf l'article Isopérimétrie).
On peut généraliser ce problème : étant donnés deux volumes Va et Vb, quelle est la surface minimale susceptible de les contenir ? L'observation incite à penser qu'il s'agit d'une double bulle, limitée par deux portions de sphère, avec un « disque » de séparation bombé ou non. Ceci n'a cependant été prouvé qu'en 1995, et encore, dans le cas de deux volumes égaux...
Beaucoup de problèmes mathématiques très ardus ont pourtant des énoncés extrêmement simples...
Les lois de Plateau
Le problème se complique singulièrement lorsque l'on a affaire à une mousse formée d'un très grand nombre de bulles accolées. Le physicien belge Joseph Plateau, dans la seconde moitié du XIXe siècle, énonça quatre lois simples, tirées de l'observation des bulles, jamais démenties, et qui portent son nom :
- tout film enfermant des bulles se compose d'éléments de surface lisses,
- la courbure moyenne de chacun de ces éléments est constante (ce ne sont pas forcément des sphères),
- lorsque trois éléments de surface se rejoignent, ils se raccordent selon une courbe régulière en tout point de laquelle leurs plans tangents forment des angles de 120°,
- lorsque ces lignes de raccordement se rejoignent, elles le font quatre par quatre et prennent alors, au point de rencontre, les quatre directions tétraédriques (comme les quatre segments qui joignent le centre d'un tétraèdre régulier à ses sommets, et dont chacun forme avec les autres des angles d'environ 109°).
Pression intérieure
Pour passer de l'extérieur à l'intérieur d'une bulle de savon, nous devons traverser deux surfaces de changement de milieu. En vertu de la loi de Laplace, nous en déduisons la pression à l'intérieur d'une bulle de savon. Elle est donnée par la formule :
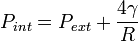
Pint étant la pression à l'intérieur de la bulle.
Pext étant la pression à l'extérieur de la bulle.
γ étant la tension superficielle.
R étant le rayon de la bulle de savon.
Couleurs observées sur une bulle de savon
Lorsque nous observons une bulle de savon en plein jour, nous pouvons voir des irisations rappelant les couleurs de l'arc-en-ciel. Pourtant le phénomène a une origine totalement différente. Ce phénomène d'iridescence est dû à des interférences entre les rayons se réfléchissant sur la surface extérieure de la bulle et les rayons se réfléchissant sur la surface intérieure de la bulle.






















































