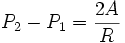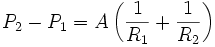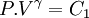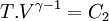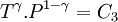Loi de Laplace - Définition
Voir aussi (en électromagnétisme) Force de Laplace.
La loi de Laplace est une loi donnant la différence de pression entre deux milieux dont la surface de séparation est incurvée.
Dans le cas particulier où la surface est localement sphérique, cette loi s'exprime par :
où
- P1 est la pression du côté convexe en pascals ;
- P2 est la pression du côté concave en pascals ;
- A est la tension superficielle à la limite de séparation en newtons par mètre ;
- R est le rayon de courbure de la surface de séparation au point considéré.
Plus généralement, la loi s'écrit :
où R1 et R2 sont les deux rayons de courbure principaux de la surface au point considéré. Dans le cas sphérique, les deux rayons de courbure principaux sont égaux : R1 = R2 = R.
On peut aussi retrouver la loi de Laplace lors d'une transformation thermodynamique d'un gaz parfait, plus précisément lors d'une transformation adiabatique et réversible, ou une transformation isentropique. Dans ce cas, la loi de Laplace est une relation qui relie la pression et le volume, la température et le volume, ou la température et la pression.
où
- P est la pression du gaz
- V est le volume occupé par le gaz
- T est la température du gaz
- γ est le coefficient de Laplace du gaz parfait (sans unité), c'est à dire le rapport des capacités thermiques à pression et volume constants
- C1,C2 et C3 étant trois constantes différentes et différentes selon les gaz parfaits.