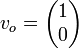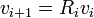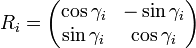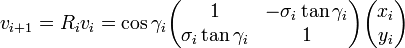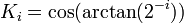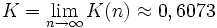CORDIC - Définition

Introduction

CORDIC (sigle de COordinate Rotation DIgital Computer : « calcul numérique par rotation de coordonnées ») est un algorithme de calcul des fonctions trigonométriques et hyperboliques, notamment utilisé dans les calculatrices. Il a été décrit pour la première fois en 1959 par Jack E. Volder. Il ressemble à des techniques qui avaient été décrites par Henry Briggs en 1624.

Il s'agit d'un algorithme de choix lorsque aucune implantation matérielle d'un multiplicateur n'est disponible (sur certains microcontrôleurs simples ou des FPGA). De plus, l'algorithme du CORDIC s'adapte bien au calcul à la chaîne. À l'origine, la programmation du CORDIC reposait sur un système binaire.

Durant les années 1970, les versions décimales du CORDIC (avec des nombres codés en BCD) commencèrent à apparaître, notamment dans les calculatrices où les critères de coût du matériel sont plus importants que la vitesse de traitement. Un autre avantage du CORDIC est sa flexibilité puisqu'il permet de calculer plusieurs fonctions avec quasiment le même code.

Description

CORDIC permet de déterminer le sinus ou le cosinus d'un angle donné en radians sous un format à virgule fixe. Pour trouver le sinus ou le cosinus d'un angle β, on recherche la coordonnée x ou y du point du cercle unité lui correspondant. CORDIC débute les calculs avec un vecteur v₀ tel que :

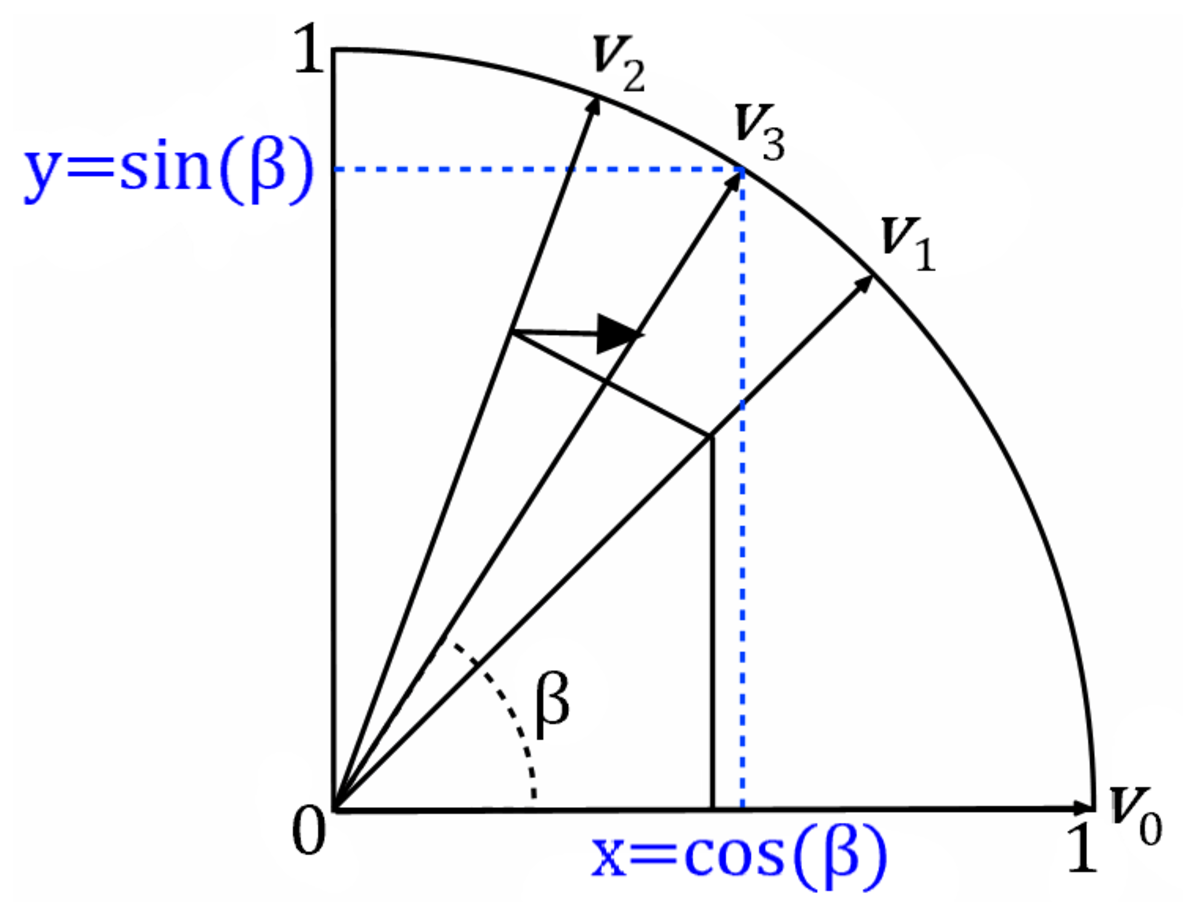
Durant la première itération, le vecteur subit une rotation de 45° dans le sens anti-horaire (sens trigonométrique) afin d'obtenir un nouveau vecteur v₁. Des itérations successives doivent engendrer une rotation du vecteur dans la bonne direction. À chaque itération, la rotation est faite d'un angle prédéterminé et moindre que le précédent. Ceci jusqu'à converger vers l'angle voulu.

Illustration de plusieurs itérations de CORDIC

Plus formellement, à chaque itération i, on calcule un nouveau vecteur grâce à la multiplication du vecteur v_i avec la matrice de rotation R_i :

La matrice de rotation s'obtient selon la formule suivante :

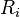
En factorisant le terme on obtient :

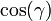
Le facteur prend les valeurs +1 ou -1 et sert à indiquer le sens de la rotation. Si l'on restreint les choix possibles pour l'angle de manière à ce que soit égal à alors la multiplication par la tangente devient une multiplication par une puissance de 2. Une opération aisée à réaliser informatiquement puisqu'en binaire il s'agit d'un décalage de bits.

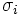
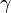
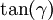
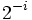
Le calcul devient :

avec

Ces coefficients K_i peuvent être ignorés pendant les itérations et factorisés en un seul coefficient multiplicatif final (dépendant de n) :

qui peut être calculé à l'avance et prémémorisé. Également, lorsque n tend vers l'infini, ce produit tend vers une constante :

Après suffisamment d'itérations, l'angle du vecteur sera proche de l'angle voulu.

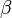
La dernière étape consiste à déterminer à chaque itération le sens de rotation, trigonométrique ou horaire (un résultat reporté sur la valeur de ). Pour ce faire, on regarde l'angle β_{n + 1} actuel du vecteur que l'on soustrait à l'angle désiré. On teste si cette différence est positive (rotation dans le sens horaire) ou négative (sens trigonométrique), de façon à s'approcher de l'angle .

,

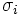
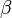
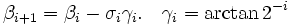
Les valeurs de γ_n sont précalculées dans une table prémémorisée de valeurs. Toutefois, pour des angles petits, on utilise l'approximation dans une représentation en virgule fixe, permettant ainsi de réduire la taille de cette table.

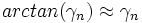
Comme illustré dans le schéma ci-dessus, le sinus de l'angle β est la coordonnée y du vecteur final v_n, alors que la coordonnée x correspond au cosinus.