Conjecture - Définition

Exemples de conjectures célèbres actuelles

Les conjectures célèbres (non résolues) comprennent à ce jour :

• la conjecture de Goldbach (formulée en 1742),
• l'hypothèse de Riemann (formulée en 1859),
• la conjecture de Syracuse (formulée dans les années 1950),
• la conjecture abc (formulée en 1985),
• la conjecture P ≠ NP,
• la conjecture des nombres premiers jumeaux qui est la plus ancienne conjecture non résolue,
• la conjecture des nombres parfaits,
• la conjecture de Birch et Swinnerton-Dyer.
• La conjecture de Legendre selon laquelle entre n² et (n+1)² existe toujours un nombre premier.

Exemples de conjectures résolues

• La conjecture de Girard, formulée en 1629, a été démontrée dans ce qu'on appelle aujourd'hui le théorème de D'Alembert-Gauss ou théorème fondamental de l'algèbre en 1813.
• la conjecture des quatre couleurs, a été démontrée en 1976 en utilisant des programmes informatiques et complètement formalisée en 2006 dans l'assistant de preuve Coq,
• le « dernier théorème de Fermat » fut démontré en 1994;
• la conjecture de Poincaré, formulée en 1904 a été résolue en 2003 positivement;
• la conjecture de Gauss qui exprimait que (où Li et la fonction d'écart logarithmique intégrale) a été infirmée par Littlewood qui a montré que la différence π(x) − Li(x) changeait de signes une infinité de fois.
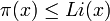
• La conjecture des nombres premiers sur la valeur asymptotique de π(x), énoncée en 1809 par Legendre, a été démontrée indépendamment par Hadamard et De La Vallée Poussin en 1896 ;
• La conjecture de Bieberbach sur les coefficients des fonctions entières injectives dans le disque unité a été démontrée en 1985 par Louis de Branges de Bourcia;
• La conjecture de Mertens, énoncée en 1897, a été réfutée en 1985 par Odlyzko et Te Riele;
• Les conjectures du mémoire de Riemann de 1859 sur la fonction ζ ont toutes été résolues avant le XX^e siècle sauf l'hypothèse de Riemann;
• Le problème de Waring a été résolu par Hilbert en 1909;
• L'hypothèse du continu a été partiellement résolue, au sens que Paul Cohen a démontré qu'elle est indépendante des axiomes de la théorie des ensembles de Zermelo-Fraenkel;
• Le problème de la quadrature du cercle par la règle non graduée et le compas seuls a été démontré impossible en 1882 par Lindemann;
• Le problème de la trisection de l'angle quelconque par la règle non graduée et le compas seuls a été démontré impossible, ainsi que le problème de la duplication du cube par les mêmes moyens.

Formulée vraisemblablement en 1637, publiée en 1670, la plus célèbre de toutes les conjectures était celle dénommée le « dernier théorème de Fermat ». Ce n'est qu'après sa démonstration par le mathématicien Andrew Wiles en 1995 que cette conjecture devint théorème. La démonstration consista à prouver un cas particulier de la conjecture de Taniyama-Shimura, problème alors en attente de résolution depuis une quarantaine d'années. On savait en effet que le dernier théorème de Fermat découlait de ce cas particulier. Le théorème complet de Taniyama-Shimura fut finalement démontré en 1999 par Breuil, Conrad, Diamond, et Taylor qui, en s'appuyant sur le travail de Wiles, remplirent par sauts de puce les cas restants jusqu'à la démonstration du résultat complet.

La plus discutée actuellement, mais aussi la plus ancienne qui puisse être datée précisément, est probablement la conjecture de Kepler, formulée par Johannes Kepler en 1611 et résolue positivement en 2003; la démonstration qui en a été publiée dans le journal Annals of Mathematics a satisfait les experts à 99 %. Une preuve satisfaisante à 100 % reste encore à produire.

Une conjecture qui a résisté pendant 66 ans est le problème de Robbins. Son intérêt réside dans le fait que la seule solution qui en existe a été produite par un programme d'ordinateur (voir W. McCune. Solution of the Robbins problem, J. Automated Reasoning, 19(3):263--276, 1997).