Convention de sommation d'Einstein - Définition

Introduction

En mathématiques et plus spécialement dans les applications de l'algèbre linéaire en physique, la convention de sommation d'Einstein ou notation d'Einstein est un raccourci de notation utile pour la manipulation des équations concernant des coordonnées.

Selon cette convention, quand l'indice d'une variable apparaît deux fois dans un terme on sous-entend la sommation sur toutes les valeurs que peut prendre cet indice. Cet indice est dit muet. Un indice non muet est dit indice réel et ne peut apparaître qu'une seule fois dans le terme en question. Généralement, ces indices sont 1, 2 et 3 pour les calculs dans l'espace euclidien ou 0, 1, 2, et 3 ou 1, 2, 3 et 4 pour les calculs dans un espace de Minkowski, mais ils peuvent avoir d'autres valeurs ou même, dans certaines applications, représenter un ensemble infini. En trois dimensions,

signifie donc

En relativité générale, l'alphabet latin et l'alphabet grec sont respectivement utilisés pour distinguer si la somme porte sur 1, 2, 3 ou 0, 1, 2, 3. Par exemple les indices i, j, ... sont utilisés pour 1, 2, 3 et μ, ν, ... 0, 1, 2, 3.

Lorsque les indices se rapportent à des tenseurs, comme en relativité générale, les indices muets doivent apparaître une fois en haut et une fois en bas; dans d'autres applications une telle distinction n'existe pas.

Définitions

Traditionnellement, on s'intéresse à un espace vectoriel V de dimension finie n et une base sur V. On peut écrire les vecteurs de base ainsi: . Dans ce cas, si est un vecteur dans V, ces coordonnées dans cette base sont .

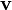
La règle de base est :

Qui, avec la convention de sommation d'Einstein, s'écrit

Dans cette expression on sous-entend que le terme de droite est additionné pour toutes les valeurs de i allant de 1 à n, car l'indice i apparaît deux fois.

L'indice i est dit muet car le résultat ne dépend pas de lui. Par exemple, pour exprimer la même chose on pourrait aussi écrire :

Dans les contextes dans lesquels l'indice doit apparaître une fois en bas et une fois en haut, les vecteurs de base s'écrivent mais les coordonnées s'écrivent vⁱ. La règle de base s'écrit alors :

.

L'intérêt de la notation d'Einstein est qu'elle s'applique à d'autres espaces vectoriels construits à partir de V en utilisant le produit tensoriel et la dualité. Par exemple, , le produit tensoriel de V par lui-même, a une base constituée de tenseurs de la forme . Tout tenseur T dans peut s'écrire :

.

V*, le dual de V, a une base qui obéit à la règle :

où est le symbole de Kronecker : vaut 1 si i = j et 0 sinon.

Ici nous avons utilisé un indice inférieur pour la base duale, comme c'est le cas lorsque les indices doivent apparaître une fois en haut et une fois en bas. Dans ce cas, si est un élément de V*, alors :

Si au contraire, tous les indices doivent être placés en base, alors une lettre différente doit être utilisée pour désigner la base duale. Par exemple:

L'utilité de la notation d'Einstein apparaît surtout dans les formules et les équations qui ne font pas mention de la base choisie. Par exemple, avec et défini comme plus haut :

.

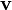
Et ceci est vrai pour toutes les bases.

Les sections suivantes contiennent d'autres exemples de telles équations.