Coupole (géométrie) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Coupole décagonale | |
|---|---|
| |
| | |
| Type | Ensemble des coupoles |
| Sommets | 3n |
| Arêtes | 5n |
| Faces | (nombre : 2n+2) 1 n-gone 1n triangles n carrés 2n-gone |
| Configuration faciale | - |
| Groupe symétrique | Cnv |
| Dual | - |
| Propriétés | convexe |
| modifier | |
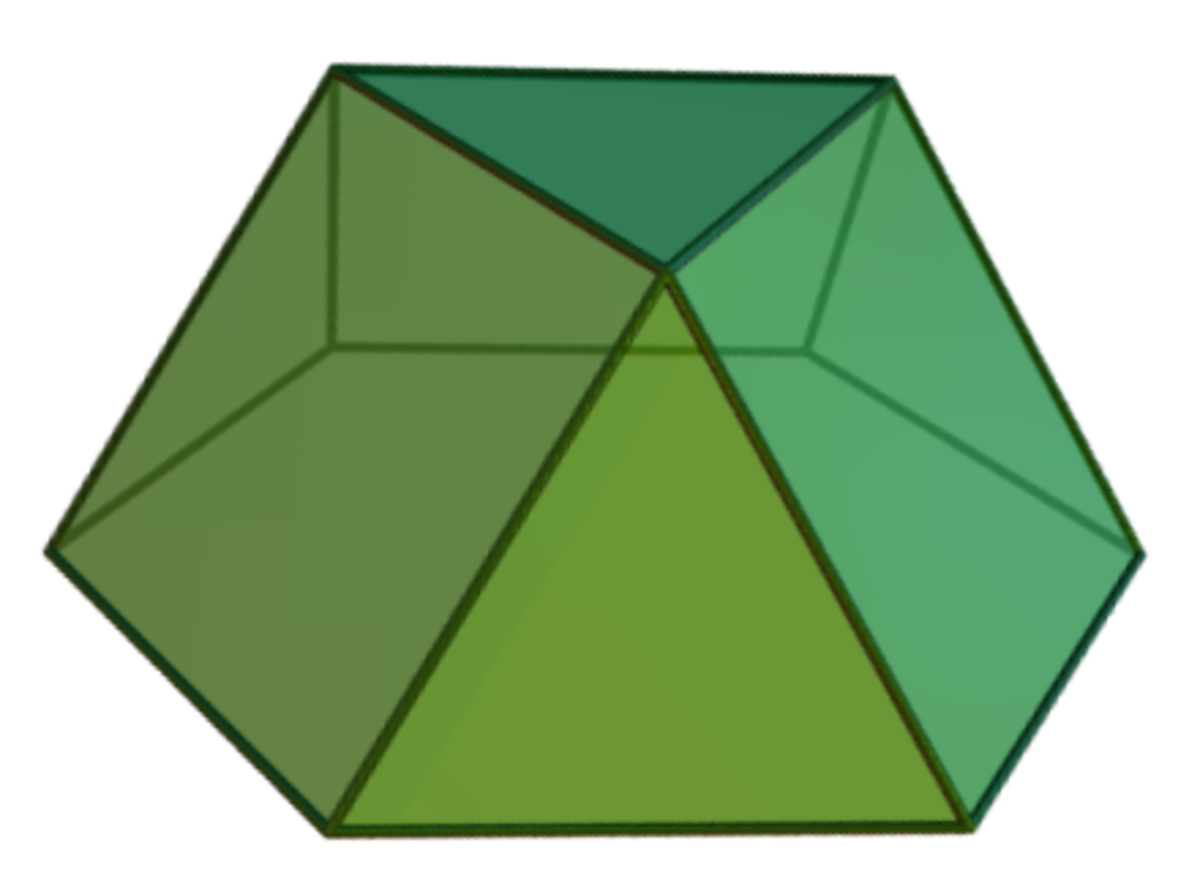
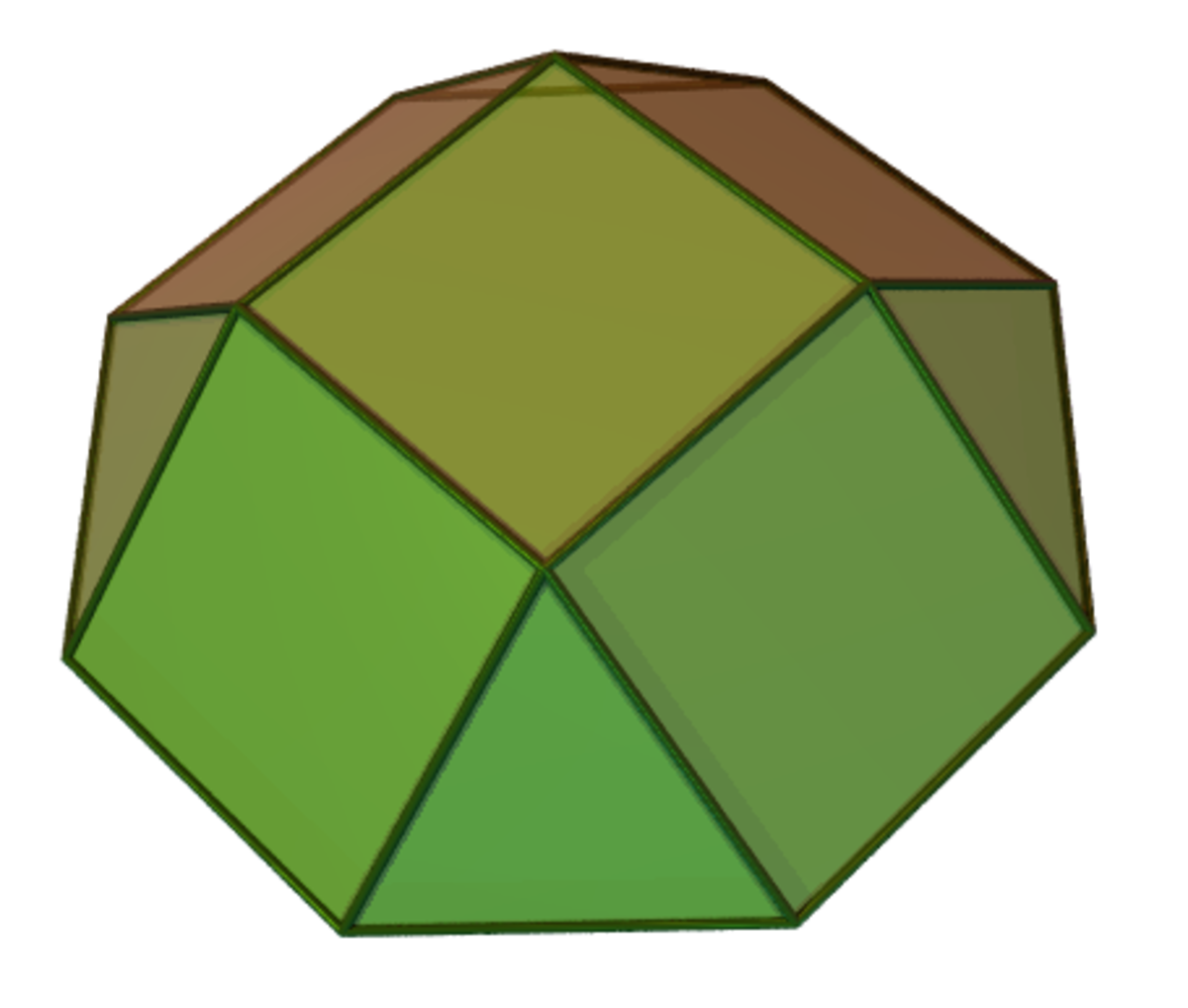
En géométrie, une coupole est un solide formé en joignant deux polygones, un (la base) avec deux fois autant d'arêtes que l'autre, par une bande alternée de triangles et de rectangles. Si les triangles sont équilatéraux et les rectangles sont carrés, alors que la base et sa face opposée sont des polygones réguliers, les coupoles hexagonales, octogonales et décagonales sont toutes comptées parmi les solides de Johnson, et peuvent être formées en prenant des sections du cuboctaèdre, du petit rhombicuboctaèdre et du petit rhombicosidodécaèdre, respectivement.
La hauteur d'une coupole 2n-gonale est égale à la hauteur d'une pyramide n-gonale (cette règle est aussi vraie pour les cas extrêmes du prisme triangulaire et de la coupole dodécagonale).
Une coupole peut être vue comme un prisme où un des polygones a été effondré par la moitié en fusionnant des sommets alternés.
Les coupoles sont une sous-classe des prismatoïdes.
Exemples
Le prisme triangulaire est aussi une coupole carrée | 
La coupole hexagonale avec des faces régulières (J3) |
La coupole octogonale avec des faces régulières (J4) | 
La coupole décagonale avec des faces régulières (J5) |
Les trois polyèdres mentionnés ci-dessus sont les seules coupoles non-triviales avec des faces régulières : la « coupole dodécagonale » est une figure plane, et le prisme triangulaire peut être considéré comme une « coupole » de degré 2 (la coupole d'un segment et d'un carré). Néanmoins, les coupoles de polygones de degrés plus élevés peuvent être construites avec des faces triangulaires et rectangulaires irrégulières.
Généralisation en dimension 4
Les coupoles peuvent être obtenues par une « expansion » des pyramides correspondantes (exemple : la pyramide carrée donne la coupole octogonale): les faces triangulaires des pyramides sont progressivement écartées par des rectangles jusqu'à ce que ceux-ci soient des carrés. La base n-gonale de la pyramide se transforme donc en une base 2n-gonale, et le sommet de la pyramide laisse place à un n-gone. Cette propriété implique que la hauteur d'une coupole 2n-gonale est la même que celle de la pyramide n-gonale.
Pour généraliser les coupoles en dimension 4, il faut donc partir d'une pyramide 4D et appliquer cette même expansion: on obtient toujours une base et un top reliés entre eux par des pyramides (qui remplacent les triangles) et des prismes (qui remplacent les carrés).
Comment savoir quelle base correspond à quel top? Il s'agit toujours d'une expansion de la base de la pyramide. Ainsi, en dimension 2, l'opération d'expansion correspondait en fait à une troncature (truncation en anglais): c'est pourquoi on reliait un n-gone à un 2n-gone; en dimension 3, l'expansion est appelée « chanfreinage » (cantellation en anglais); si on voulait élargir jusqu'en dimension 5, l'expansion prend le nom (en anglais) de « runcination » puis « sterication » (voir la page anglaise Expansion (geometry)).
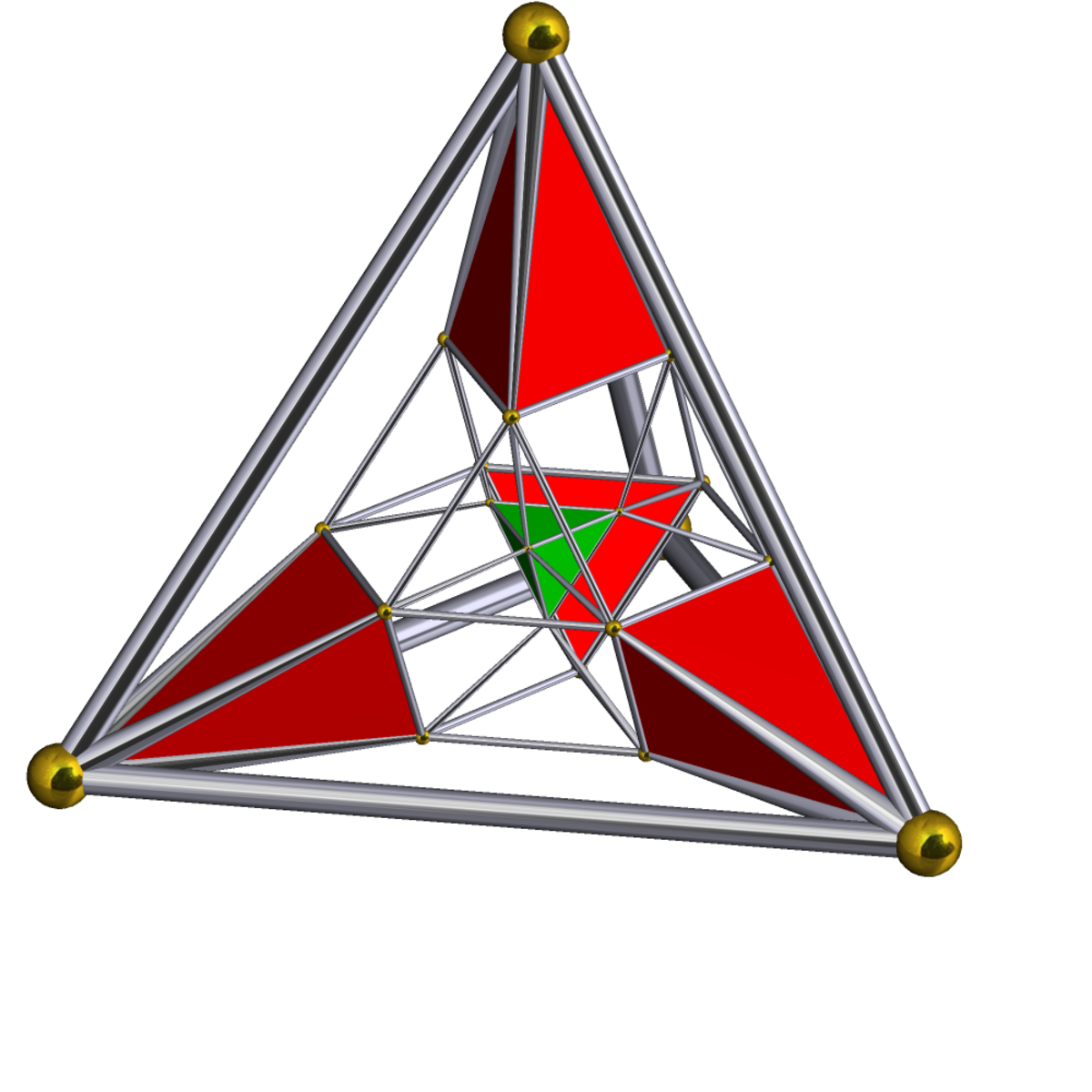
Ainsi, l'exemple le plus simple d'une pyramide régulière 4D, le pentachore, a pour base un tétraèdre. Le chanfreinage d'un tétraèdre donne un cuboctaèdre. La coupole correspondante est donc la coupole tétraédrique, ayant pour base un cuboctaèdre et pour top un tétraèdre. De même que 2 coupoles hexagonales donnent un cuboctaèdre, 2 coupoles tétraédriques donnent un pentachore « runciné » (runcinated pentachoron en anglais).
Il existe en tout 4 hyperpyramides régulières, il existe donc 4 hypercoupoles régulières: la coupole tétraédrique, la coupole cubique, la coupole octaédrique et la coupole dodécaédrique.
