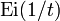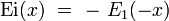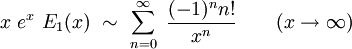Développement asymptotique - Définition

Introduction

En mathématiques, un développement asymptotique d'une fonction f donnée dans un voisinage fixé est une somme finie de fonctions de références qui donne une bonne approximation du comportement de la fonction f dans le voisinage considéré. Le concept de développement asymptotique a été introduit par Poincaré à propos de l'étude du problème à N corps de la mécanique céleste par la théorie des perturbations.

La somme étant finie, la question de la convergence ne se pose pas. On parle parfois par abus de langage de « série asymptotique » pour une somme comprenant une infinité de termes. Cette somme infinie est le plus souvent formelle, car la série est en général divergente.

Analyse asymptotique : comportement équivalent

Introduction

L'analyse asymptotique est une méthode d'analyse qui permet de classer les comportements de fonctions dans un voisinage donné en se concentrant sur certaines tendances caractéristiques. On l'exprime en général au moyen d'une relation d'équivalence. Par exemple, soient deux fonctions complexes f et g d'une variable réelle x dont on souhaite étudier le comportement au voisinage d'un point x₀. On écrira :

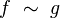
pour traduire le fait que :

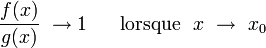
Ceci défini une relation d'équivalence entre fonctions, et la classe d'équivalence de la fonction f consiste en toutes les fonctions g qui possèdent un comportement similaire à f dans le voisinage du x₀. On est ainsi amené à définir un ensemble de fonctions « simples », qui vont servir de référence pour établir des comparaisons. Remarquons tout d'abord qu'on peut toujours se ramener à étudier le voisinage de . En effet, étudier le comportement de f au voisinage du x₀ est équivalent à étudier le comportement de :

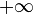
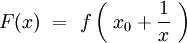
au voisinage de . On peut donc se limiter à un ensemble de fonctions de comparaison dans un voisinage de .

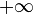
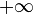
Fonctions de comparaison

Définitions

On considère comme connues au voisinage de les fonctions de l'un des types suivant :

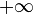
• la fonction constante 1 ;
• x^α, où  ;
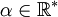
• (lnx)^β où ;
• , où  ;

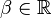
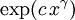
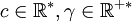
ainsi que leurs produits, c’est-à-dire toute fonction de la forme :

où P(x) est de la forme :

Propriétés

Si on désigne par E l'ensemble de ces fonctions de comparaisons, on a les propriétés suivantes :

• Toute fonction de E est positive dans un voisinage de  ;
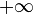
• En dehors de la fonction constante 1, toute fonction de E tend soit vers zéro, soit vers lorsque x tend vers  ;
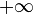
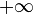
• Tout produit de fonctions de E appartient à E ;
• Si f appartient à E, alors f^λ appartient à E pour tout λ réel ;

Les deux dernières propriétés montrent en particulier que le quotient de deux fonctions de E appartient à E.

Si g est une fonction de E, on considère également connue toute fonction complexe f de la forme f = c g où c est un nombre complexe.

Partie principale d'une fonction

Soit f la fonction dont le comportement est à analyser au voisinage de . Si on peut trouver une fonction g₁ de E telle que f/g₁ ait une limite finie c₁ non nulle , on dit que c₁ g₁ est la partie principale de f par rapport à E, et on écrit :

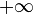
en utilisant les notations de Landau. (Toute fonction de E est sa propre partie principale.)

« Série asymptotique »

Introduction

Pour un développement comprenant une infinité de termes, on parle parfois par abus de langage de « série asymptotique ». Cette somme infinie est le plus souvent formelle, car la série est en général divergente.

Par exemple, pour une fonction f lisse au voisinage d'un point x₀, on peut pousser son développement de Taylor aussi loin que l'on veut. On peut alors se poser le problème de la convergence de la série de Taylor obtenue, et de la relation entre sa somme et la fonction f de départ. Ce problème est sans rapport avec le comportement asymptotique de la fonction f dans le voisinage de x₀.

Exemple

Soit la fonction f(x) définie par la série convergente pour |x| < 1 :

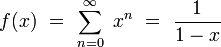
La dernière expression de f permet d'étendre sa définition à tout le plan complexe privé de x = 1, notamment là où la série originale est divergente. Multiplions alors par e ^{− x / t} et intégrons ; on obtient formellement :

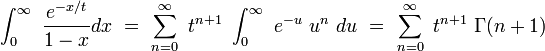
où Γ(z) est la fonction gamma d'Euler. L'intégrale du membre de gauche s'exprime en fonction de l'exponentielle intégrale Ei(x), et on obtient alors le développement asymptotique de cette fonction au voisinage de t=0 :

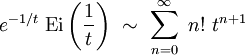
Pour tout t non-nul, le membre de droite ne converge pas. En revanche, pour t non-nul « petit », on obtient en tronquant la somme à un nombre fini de termes une bonne représentation de la fonction . Le changement de variable : x = 1 / t et la relation fonctionnelle : conduit au développement asymptotique :