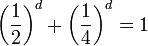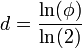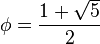Dimension de Hausdorff - Définition

Exemples

Triangle de Sierpinski, de dimension de Hausdorff ..

• Un ensemble dénombrable est de dimension nulle.
• Le cercle est de dimension de Hausdorff 1.
• Dans , la dimension d'un ensemble de mesure de Lebesgue non nulle est n.
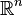
• Le graphe d'une fonction d'une variable réelle lipschitzienne est de dimension de Hausdorff 1. Si la fonction est a-höldérienne, alors la dimension de Hausdorff de son graphe est comprise entre 1 et 2 - a.
• La dimension de Hausdorff de l'ensemble triadique de Cantor est .
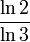
• La dimension de Hausdorff du triangle de Sierpiński est .
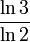
• La dimension de Hausdorff du tapis de Sierpiński est .
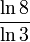
• La trajectoire du mouvement brownien en dimension 2 est presque sûrement de dimension 2.

Calcul pratique dans un cas particulier classique

Si est une partie d’un espace vectoriel réel qui vérifie la propriété suivante :

« Il existe similitudes de rapports telles que soient disjoints deux à deux et que leur union soit isométrique avec . »

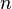
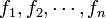
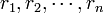
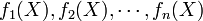
On a alors la relation :

, où est la dimension de .

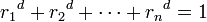
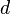
Cela découle de la propriété suivante des mesures de Hausdorff :

« Pour tout λ positif, . »

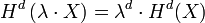
et de l'invariance par isométrie. Cela offre un moyen simple de calculer les dimensions de fractales classiques, telles le flocon de Koch, le tapis de Sierpinski, etc.

Exemple

• L’ensemble de Cantor est constitué de deux ensembles de Cantor trois fois plus petits ; les deux similitudes sont donc ici des homothéties de rapports 1/3, composées avec des translations.

Donc , ce qui donne : .

L'ensemble de Cantor asymétrique

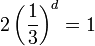
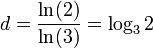
• L’ensemble de Cantor asymétrique est constitué de deux ensembles de Cantor, l'un deux fois plus petit, l'autre quatre fois plus petit. Les deux similitudes sont donc ici des homothéties de rapports respectifs 1/2 et 1/4, composées avec des translations.

Donc , ce qui conduit à : , où est le nombre d'or.