E=mc2 - Définition
La liste des auteurs de cet article est disponible ici.
Cas d'une particule de masse nulle
Le cas d'une particule de masse nulle découle des formules précédentes, et notamment de :
Si une particule a une vitesse égale à c son énergie est :
Par conséquent sa masse est nulle puisqu'elle est donnée par la formule :
Inversement si une particule a une masse nulle son énergie est E = pc et par conséquent v = c.
En physique des particules, plusieurs particules ont une masse nulle et se déplacent à la vitesse c, dont les photons, qui transportent le rayonnement électromagnétique, et les bosons de jauge, qui transmettent les autres interactions fondamentales du modèle standard. Le neutrino a longtemps été considéré comme une particule de masse nulle mais des expériences récentes comme celle de Super-Kamiokande font penser que cette masse serait toute petite mais pas nulle. Dans le cadre de la relativité générale les ondes gravitationnelles se déplacent aussi à la vitesse de la lumière et la particule associée, appelée graviton, devrait être de masse nulle.
Néanmoins à ce jour, et contrairement aux autres particules citées, ni le graviton ni le rayonnement gravitationnel associé n'ont été observés expérimentalement. Seul le rayonnement gravitationnel a été mis indirectement en évidence, par ses effets, dans la réduction des orbites d'un couple de pulsars.
Autre notation
En notant m la masse de la particule et E son énergie au repos l'équation d'Einstein s'écrit :
- E0 = m0c2.
On introduit alors parfois la quantité :
qui n'est plus la vraie masse m, mais qui, mesurant l'inertie de la particule, est parfois appelée masse inerte.
Dans ces conditions la formule écrite plus haut « E=γmc2 » donnant l'énergie de la particule prend la même forme :
l'expression étant alors valable même dans le cas où le corps n'est pas au repos.
Cependant cet emploi est fortement déconseillé par les spécialistes. Ils font remarquer en effet que la vraie masse au repos, notée ici m, possède une signification physique indépendante du repère choisi car son carré est l'invariant du vecteur énergie-impulsion (en unités relativistes). Or cette propriété majeure n'est pas partagée par la pseudo-masse inerte m, qui elle dépend du repère choisi et ne mérite pas le nom de masse, car elle ne correspond plus à une véritable grandeur physique. Au mieux on peut considérer la formule E = mc2 ainsi écrite comme un moyen mnémotechnique pour retenir l'expression de l'énergie mais la signification physique de cette formulation est faible.
Énergie d'une particule
L'énergie totale d'une particule isolée (qui dépend, rappelons-le, du repère choisi) peut s'écrire comme la somme de son énergie au repos mc2 et de son énergie cinétique K.
On a donc :
L'énergie cinétique devient :
- Aux faibles vitesses (c'est-à-dire petites devant celle de la lumière), on obtient :
qui n'est autre que l'énergie cinétique classique.
- Pour les vitesses très proches de celle de la lumière, l'énergie au repos de la particule s'avère négligeable devant l'énergie cinétique.
Comme on peut écrire :
l'énergie totale devient :
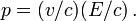
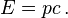
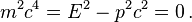
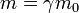
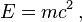
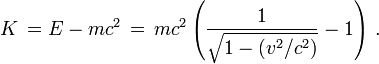
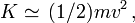
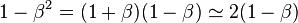
![E \simeq K = \frac{mc^2}{\sqrt{2(1-\beta)}}\equiv \frac{mc^2}{\sqrt{2[1-(v/c)]}}\,.](https://static.techno-science.net/illustration/Definitions/autres/0/094a0daad581de7f363c7475e72a50b1_4d7941870631664150159ca7503ea08d.png)

















































