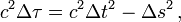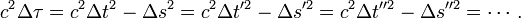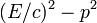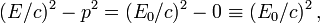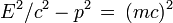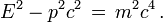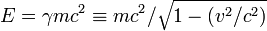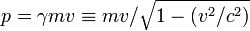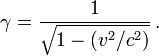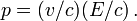E=mc2 - Définition

Introduction

Avant Einstein

Avec Einstein

En physique des particules

Méta

Sculpture de « E=mc² », à Berlin.

L'équation E=mc² a été formulée en 1905 par Albert Einstein dans le cadre de la relativité restreinte. Elle signifie qu'une particule isolée et au repos de masse m possède, du fait de cette masse, une énergie E, appelée énergie de masse donnée par le produit de m par le carré de la vitesse de la lumière.

Cette relation a fortement marqué les esprits car elle montre que, du fait de l'énormité du facteur c², une masse même petite à l'échelle humaine (par exemple 1 gramme) possède une quantité considérable d'énergie (environ 10¹⁴ joules pour une masse d'un gramme). Cependant, il faut se méfier des conversions directes : d'autres lois (conservation de la charge, du nombre baryonique...) montrent qu'on ne peut espérer convertir arbitrairement la matière en énergie suivant cette formule (on peut convertir en énergie une quantité égale de matière et d'antimatière).

Historique

C'est avec le dernier des articles publiés lors de son annus mirabilis qu'Einstein exprime pour la première fois ce qui deviendra son équation célèbre : « Si un corps perd une énergie L sous forme de rayonnement, sa masse diminue de L/c² ».

Dans ce texte, il produit une première démonstration pour le cas général de ce principe d'équivalence qui jusque-là n'avait été démontré que dans des cas particuliers. Il en proposera par la suite deux autres, en 1934 et en 1946.

L'équation E=mc² fait partie des apports que certains contestent à Einstein dans le cadre de la controverse sur la paternité de la relativité.

Formulation générale

Si la formule E = mc² concerne une particule au repos, c'est-à-dire une particule dont la vitesse est nulle dans le référentiel choisi, que devient cette expression dans un autre référentiel, avec une particule animée d'une vitesse v ?

Alors que la géométrie euclidienne raisonne sur des points repérés dans l'espace par trois coordonnées, la relativité restreinte raisonne sur des événements repérés dans l'espace-temps par quatre coordonnées, une de temps et trois d'espace. De même que la distance euclidienne entre deux points est invariante par changement de repère, de même la théorie relativiste stipule que le carré de l'intervalle d'espace-temps défini par :

où Δt représente l'intervalle de temps entre les deux événements et Δs la distance, est invariant par changement de repère. Autrement dit quand on mesure les coordonnées des mêmes événements dans plusieurs repères (t, x, y, z)), (t', x', y', z'), (t", x", y", z"),… différents la quantité suivante ne change pas de valeur :

Alors que la mécanique newtonienne considère d'une part l'énergie et d'autre part la quantité de mouvement d'un corps en mouvement, la relativité unifie ces deux concepts dans un objet unique : le quadrivecteur énergie-impulsion. Ce vecteur à quatre dimensions a pour composante temporelle l'énergie E/c de la particule et pour composante spatiale son vecteur impulsion (ou quantité de mouvement) à trois dimensions. Comme il est le pendant du vecteur impulsion mv de la mécanique classique (produit de la masse par la vitesse) il est égal à m u où u est maintenant le quadrivecteur vitesse.

De même que le carré de l'intervalle d'espace-temps était invariant par changement de coordonnées, de même l'est le carré de la norme du quadrivecteur énergie-impulsion. Autrement dit la quantité :

est indépendante du repère dans lequel on l'évalue. Mais séparément, l'énergie et l'impulsion en dépendent.

Dans le repère propre de la particule, celui où elle est au repos, la vitesse, et donc l'impulsion, est nulle. Si on note E l'énergie dans ce repère propre l'invariance de la quantité précédente s'écrit :

La valeur de E nous est donné par le fameux mc² de sorte que l'on aboutit à l'équation capitale suivante :

ou encore :

La théorie montre que dans un repère où la vitesse de la particule est v l'énergie et la quantité de mouvement sont données par les formules :

avec la notation classique,

On vérifie que E² − p²c² = m²c⁴ et on déduit de ces formules la relation importante entre énergie et impulsion :