Forme trace - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques la forme trace est un concept associé à la théorie de Galois et à la théorie algébrique des nombres.
Si une extension finie L d'un corps K est considéré comme un espace vectoriel, la forme trace apparaît comme une forme bilinéaire de L.
Dans le cas un anneau d'entiers algébriques, la forme trace possède une propriété remarquable, son déterminant ne dépend pas de la base choisie. Cette propriété permet de définir le discriminant d'un anneau d'entiers.
La forme trace, à travers la notion de discriminant, permet d'établir des démonstrations d'arithmétique comme le caractère fini du groupe des classes d'idéaux ou le théorème des unités de Dirichlet.
Définition et exemple
Définition
Ici K est un corps commutatif, L une extension de dimension finie d, l un élément de L et φl l'endomorphisme du K espace vectoriel L qui à x associe l.x.
-
- La trace de L sur K de l'élément l est égal à la trace de l'endomorphisme φl. Elle est en général notée TrL/K.
Cette définition est à l'origine d'une forme bilinéaire sur L en tant que K espace vectoriel :
-
- La forme trace de L sur K est la forme bilinéaire du K espace vectoriel L, qui à (l1, l2) associe la trace de l1.l2.
Exemple
L'anneau des entiers de Gauss correspond à l'anneau des entiers de la forme x + i.y ou x et y sont des entiers relatifs et i l'unité imaginaire. Soit a (resp. b) un entier de Gauss égal à α + i.β (resp. γ + iδ), dans la base (1, i ) les matrices Ma Mb et Mab de φa, φb et φab sont égales à :
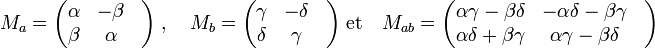
On en déduit, si Ψ désigne la matrice de la forme trace et discr (OK) de discriminant de l'anneau :
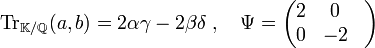
Discriminant d'un anneau
Définition
Dans cette partie, K désigne une extension finie du corps des nombres rationnels. OK désigne l'anneau de tous les entiers algébriques de K encore appelé fermeture intégrale de Z dans K. Un entier algébrique est un nombre algébrique dont le polynôme minimal (unitaire) est à coefficients dans Z.
On remarque que tout isomorphisme α de OK, considéré comme un Z module, possède un déterminant inversible dans Z. En effet :
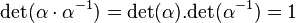
Le déterminant d'un isomorphisme est donc égal soit à 1 soit à -1. Le changement de base d'une forme bilinéaire ne modifie pas le déterminant. Ce qui permet d'établir la définition suivante :
-
- Le discriminant d'un anneau de OK est égal au déterminant de sa forme trace.
Exemple
La connaissance d'une expression matricielle de la forme trace des entiers de Gauss permet un calcul du discriminant :
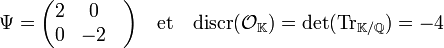
Le discriminant de l'anneau est égal à -4. Il est possible de le calculer autrement, le polynôme X 2 + 1 permet de définir le corps K des rationnels de Gauss. En effet, K est isomorphe au quotient de l'anneau Q[X] des polynômes à coefficients rationnels par l'idéal engendré par X 2 + 1. Le discriminant du polynôme X 2 + 1 est aussi égal au discriminant de l'anneau. Cette propriété est générale.
Le calcul du discriminant d'une fermeture d'un corps quadratique est donnée dans l'article associé dans l'article Idéal de l'anneau des entiers d'un corps quadratique. Ce cas particulier est plus simple et permet une approche didactique de l'intérêt de ce concept.
Propriétés
Discriminant d'un idéal
La définition précédente s'applique aux sous-anneaux de OK. La proposition suivante permet de calculer son discriminant :
-
- Le discriminant d'un sous-anneau M de OK est donnée par la formule suivante :
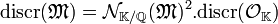
L'idéal M est un Z module de même dimension que OK, en conséquence il existe une application linéaire bijective f de OK en tant que Z module dans M. La démonstration est donnée dans l'article Norme (arithmétique). Soient F la matrice de f dans une base B de OK, x et y deux vecteurs de M et X et Y leur vecteur colonne dans la base de M, image de B par f. On a l'égalité matricielle :
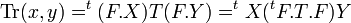
On en déduit :
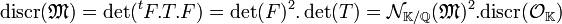
Discriminant et polynôme
Le discriminant d'un anneau OK possède une définition bien différente de celle d'un discriminant de polynôme à une indéterminée. Les deux définitions sont néanmoins corrélées.
Soit A un sous-anneau de OK et a un élément générateur de l'anneau, c'est-à-dire que Z[a] la Z algèbre engendrée par a est égale à l'anneau A. Soit P(X) le polynôme minimal de a. La proposition suivante montre la relation entre les deux discriminants :
-
- Le discriminant de A est égal au discriminant du polynôme minimal P(X) de a.
Remarquons dans un premier temps que P(X) est un polynôme irréductible et séparable. En effet, si P(X) n'est pas irréductible l'un de ses facteurs, de degré strictement plus petit que celui de P(X) annule a et P(X) ne peut être un polynôme minimal. De plus le corps des nombres rationnels est parfait, ce qui signifie qu'un polynôme minimal n'admet jamais de racine double.
Soit d la dimension de l'anneau A, la famille (1, a, a2, ..., ad-1) est une base de A. Considérons, comme dans la boite déroulante du paragraphe sur les propriétés, la matrice M de la forme trace dans la base précédente et E le D espace vectoriel produit tensoriel du Q espace vectoriel K et de D le corps de décomposition de K. La démonstration précédente montre que l'endomorphisme de matrice M est diagonalisable dans E et que l'expression matricielle de la forme trace est le produit de la transposée de A avec A, si A est égal à (λ ki ) où λ k désigne la kième racine de P(X). Le calcul d'un déterminant d'une matrice de Vandermonde montre que :
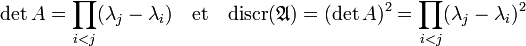
Comme le coefficient du monôme dominant du polynôme P(X) est égal à un, on retrouve exactement l'expression du discriminant du polynôme minimal, ce qui termine la démonstration.

















































