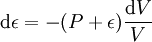Fluide parfait - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mécanique des fluides, un fluide est dit parfait s'il est possible de décrire son mouvement sans prendre en compte les effets de viscosité et de la conductivité thermique. Avec en sus l'hypothèse, de validité très générale, de conservation de la masse, le mouvement du fluide est donc isentropique.
Mathématiquement cela revient à annuler les termes correspondants dans l'équation de Navier-Stokes, on obtient ainsi l'équation d'Euler des fluides. Ce sont le produit des coefficients de viscosité et de conductivité thermique (et pas seulement ces coefficients) avec respectivement les cisaillements de vitesse et les gradients thermiques, qui doivent être négligeables.
Tous les fluides ayant une viscosité (sauf un superfluide, ce qui en pratique ne concerne guère que l'hélium à très basse température et l'intérieur d'une étoile à neutrons), le fluide parfait ne peut être qu'une approximation pour une viscosité tendant vers zéro. Cela revient à faire tendre le nombre de Reynolds vers l'infini. Ce type de situation est cependant très courant, par exemple en aérodynamique (où des nombres de Reynolds très grands sont en jeu). Dans ces conditions, les zones de cisaillement important (où la viscosité et la turbulence sont influentes) sont concentrées dans des espaces restreints, appelés couches limites, et la description globale de l'écoulement par un fluide parfait peut être adéquate.
En cosmologie, les différentes formes de matière qui emplissent l'univers peuvent être considérées, du moins aux échelles où l'univers est homogène comme des fluides parfaits. Comme l'écoulement d'un fluide parfait est isentropique, l'expansion de l'univers est parfois décrite comme étant adiabatique, s'identifiant sous certains aspects à la détente d'un gaz sans échange de chaleur avec l'extérieur.
Propriétés essentielles
Un fluide parfait obéit à l'équation de conservation de la masse, à l'équation d'Euler sans viscosité, ces deux équations formant les équations de base des fluides non dissipatifs, ainsi qu'à une version du premier principe de la thermodynamique, ce deux aspects (mécanique des fluides et thermodynamique) étant intimement liés.
Les deux premières équations s'écrivent, en notant ρ la masse volumique du fluide, P sa pression et v sa vitesse :
-
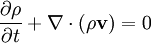
-
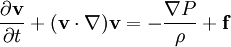
où
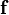
-
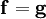
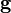
Formalisme mathématique
Un fluide parfait peut être décrit à l'aide d'un tenseur énergie impulsion T. À partir duquel on peut retrouver les équations (conservation de la masse et Euler, plus premier principe de la thermodynamique) auxquelles obéit le fluide parfait. Celui-ci s'écrit
-
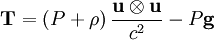
ou, en termes de composantes,
-
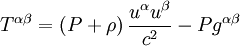
où ρ représente la densité d'énergie du fluide, somme de sa densité d'énergie interne ε et de sa densité d'énergie de masse μc2, μ étant la masse volumique de l'élément de fluide et c la vitesse de la lumière, u la quadrivitesse du fluide (c'est-à-dire la vitesse d'ensemble de cet élément), et g le tenseur métrique. La relativité restreinte et la relativité générale stipulent que le tenseur énergie impulsion d'un fluide est « conservé », c'est-à-dire que sa divergence est nulle. Cette équation s'écrit, en termes de composantes,
-
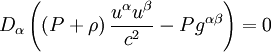
D représentant la dérivée ordinaire (en relativité restreinte) ou la dérivée covariante (en relativité générale). Le calcul donne alors
-
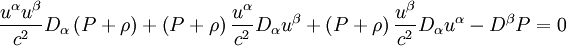
C'est cette équation qui permet de retrouver les trois équations précitées.
La quantité uαDαX mesure la variation d'une quantité X le long de la trajectoire de l'élément de fluide. Elle correspond donc à la variation de cette quantité transportée par l'élément de fluide. On la note communément d / dτ, τ étant le temps propre associé à l'élément de fluide. On obtient ainsi
-
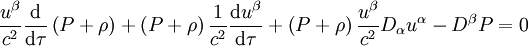
En effectuant le produit scalaire de cette équation avec la quadritesse, il vient alors, en notant par un point la dérivée par rapport à τ,
-
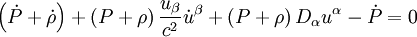
La quadrivitesse ayant une norme constante, uβuβ = c2, une quantité du type
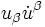
-
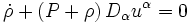
Le terme Dαuα, habituellement noté θ est appelé expansion de l'élément de fluide. Dans la limite non relativiste, il correspond à la divergence du vecteur vitesse, ce qui correspond au taux de variation de son volume. Ainsi, on a
-
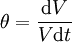
ce qui permet de réécrire l'équation en
-
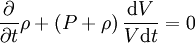
Enfin, l'hypothèse de conservation du nombre de particules s'écrit
-
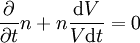
où n représente la densité de particules. Elle est reliée à sa densité d'énergie de masse par la formule
-
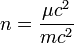
m étant la masse des particules. Cette équation s'interprète par le fait que le nombre de particules de l'élément de fluide étant contant, la variation de la densité de celles-ci le long de l'écoulement est uniquement due à la variation du volume de l'élément En pratique, si l'on repasse en termes de coordonnées, la densité de particules est une fonction des coordonnées d'espace et de temps,
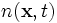
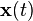
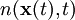
-
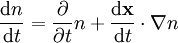
Ainsi, on obtient
-
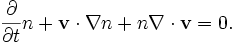
que l'on peut regrouper en
-
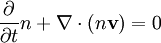
Ainsi, l'équation initiale laisse uniquement
-
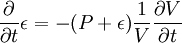
soit comme annoncé
-