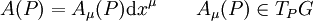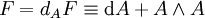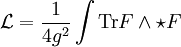Équations de Yang-Mills - Définition

Introduction

Une théorie de Yang-Mills est un type de théorie de jauge non abélienne, dont le premier exemple a été introduit dans les années 1950 par les physiciens Chen Ning Yang, et Robert Mills pour obtenir une description cohérente de l'interaction faible au sein des noyaux atomiques. Depuis, il a été réalisé que ce type de théorie, une fois incorporé dans le cadre de la théorie quantique des champs, permet une description de l'ensemble des interactions fondamentales de la physique des particules et est à la base conceptuelle du modèle standard.

Son expression mathématique moderne fait appel aux outils de la géométrie différentielle et des espaces fibrés. Bien que la formulation et le cadre géométrique de la théorie de Yang-Mills classique soient bien connus depuis longtemps, deux propriétés fondamentales n'ont toujours pas été démontrées mathématiquement :

• d'une part l’existence d'une théorie quantique des champs cohérente, fondée sur une théorie de Yang-Mills ;
• d'autre part l'existence d'un gap de masse qui ne permet l'observation des gluons, particules élémentaires de la théorie quantique associés à toute théorie de Yang-Mills, que sous forme de combinaisons massives appelées boule de glue (glueball en anglais). Ce problème non résolu est intimement lié à celui du confinement de couleur qui affirme que seuls sont observables les états quantiques de charge nulle.

La résolution de ces deux points constitue l'un des problèmes du prix du millénaire.

En dehors de ces aspects associés à la physique quantique, la théorie de Yang-Mills classique est hautement non linéaire et les équations de Yang-Mills qui lui sont associées sont très difficiles à résoudre de façon exacte en dehors de cas particuliers. C'est cette non-linéarité, associée à une structure géométrique riche, qui donne aux théories de Yang-Mills toute leur complexité et en fait un sujet de recherche actif à la fois en mathématiques et en physique théorique.

Formulation technique et lagrangien de Yang-Mills

Pour définir une théorie de Yang-Mills il faut commencer par se donner un groupe de jauge G qui est un groupe de Lie et représente physiquement le groupe de symétrie locale de la théorie. L'invariance locale signifie que les équations de Yang-Mills seront inchangées sous l'action de transformations de G sur les champs physiques en chaque point de l'espace-temps.

Pour décrire la théorie, le meilleur point de vue est alors d'incorporer l'espace-temps et le groupe G au sein d'une même entité géométrique appelée espace fibré en G. On peut visualiser cet espace fibré par la donnée d'une copie du groupe G au-dessus de chaque point de l'espace-temps.

Une fois cet espace construit l'outil fondamental de l'analyse est la donnée d'une connexion A qui est un objet analogue au potentiel vecteur de la théorie électromagnétique. D'un point de vue mathématique une connexion est ce qui permet de définir un transport parallèle sur l'espace-fibré. D'un point de vue de physique quantique, et pour prendre l'exemple plus simple de l'électromagnétisme, la connexion est ce qui permet de connaitre l'évolution de la phase d'une particule chargée, comme un électron en mouvement par exemple.

Pour définir complètement cette connexion, on peut la voir comme une forme différentielle sur l'espace-temps à valeur dans l'espace tangent du groupe de Lie G, ce qu'on appelle l'algèbre de Lie de G. En tout point P de l'espace-temps elle peut s'écrire

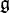
où x^μ sont des coordonnées sur l'espace-temps.

En première approche on peut aussi visualiser A_μ comme la donnée d'une matrice (dans la représentation adjointe de G) en chaque point de l'espace-temps.

On peut alors introduire le lagrangien de Yang-Mills, duquel découlent de nombreuses équations. Il est formulé en termes de la courbure F de la connexion A qui est exprimée par

et s'écrit

où Tr est la trace dans la représentation adjointe l'algèbre de Lie de . g est le seul paramètre libre de la théorie et correspond à la constante de couplage de la théorie de Yang-Mills.

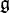
L'utilisation de ce lagrangien fait intervenir des équation aux dérivées partielles, dont l'existence ou l'unicité des solutions est inconnue dans le cas général. On peut toutefois, en imposant certaines conditions initiales, lever ce problème. Néanmoins, cela n'est pas satisfaisant d'un point de vue physique, car de telles conditions ne correspondent pas (ou ne permettent pas de se ramener) à celles de l'expérience.