Groupe de symétrie - Définition

Introduction

Un tétraèdre régulier peut être placé dans 12 positions distinctes par une seule rotation. Celles-ci sont illustrées ci-dessus dans le format d'un graphe de cycles avec des rotations à 180° par rapport à une arête (flèches bleues) et à 120° par rapport à un sommet (flèches rouges) qui permutent le tétraèdre dans toutes les positions. Les 12 rotations forment le groupe (de symétrie) de rotation de la figure.

Le groupe de symétrie d'un objet (image, signal, etc.) est le groupe de toutes les isométries sous lesquelles cet objet est globalement invariant, l'opération de ce groupe étant composition. C'est un sous-groupe du groupe euclidien (en), qui est le groupe des isométries de l'espace affine euclidien ambiant.

(Si cela n'est pas indiqué, nous considérons ici les groupes de symétrie en géométrie euclidienne, mais le concept peut aussi être étudié dans des contextes plus larges, voir .)

Les "objets" peuvent être des figures géométriques, des images et des motifs, tel que les motifs de papier peint (en). La définition peut être rendue plus précise en précisant ce que l'on entend par image ou motif, par exemple une fonction de position avec des valeurs dans un ensemble de couleurs. Pour la symétrie des corps en 3D, par exemple, on peut aussi vouloir prendre en compte la composition physique. Le groupe des isométries de l'espace induit une action de groupe sur les objets qu'il contient.

Le groupe de symétrie est quelquefois appelé le groupe de symétrie complet afin de souligner qu'il inclut les isométries qui renversent l'orientation (comme les réflexions, les réflexions glissées et les rotations impropres) sous lesquelles la figure est invariante. Le sous-groupe des isométries qui conservent l'orientation (i.e. les translations, les rotations et les compositions de celles-ci) et qui laissent la figure invariante est appelé son groupe de symétrie propre. Le groupe de symétrie propre d'un objet est égal à son groupe de symétrie complet si et seulement si l'objet est chiral (et ainsi, il n'existe pas d'isométries renversant l'orientation sous lesquelles il est invariant).

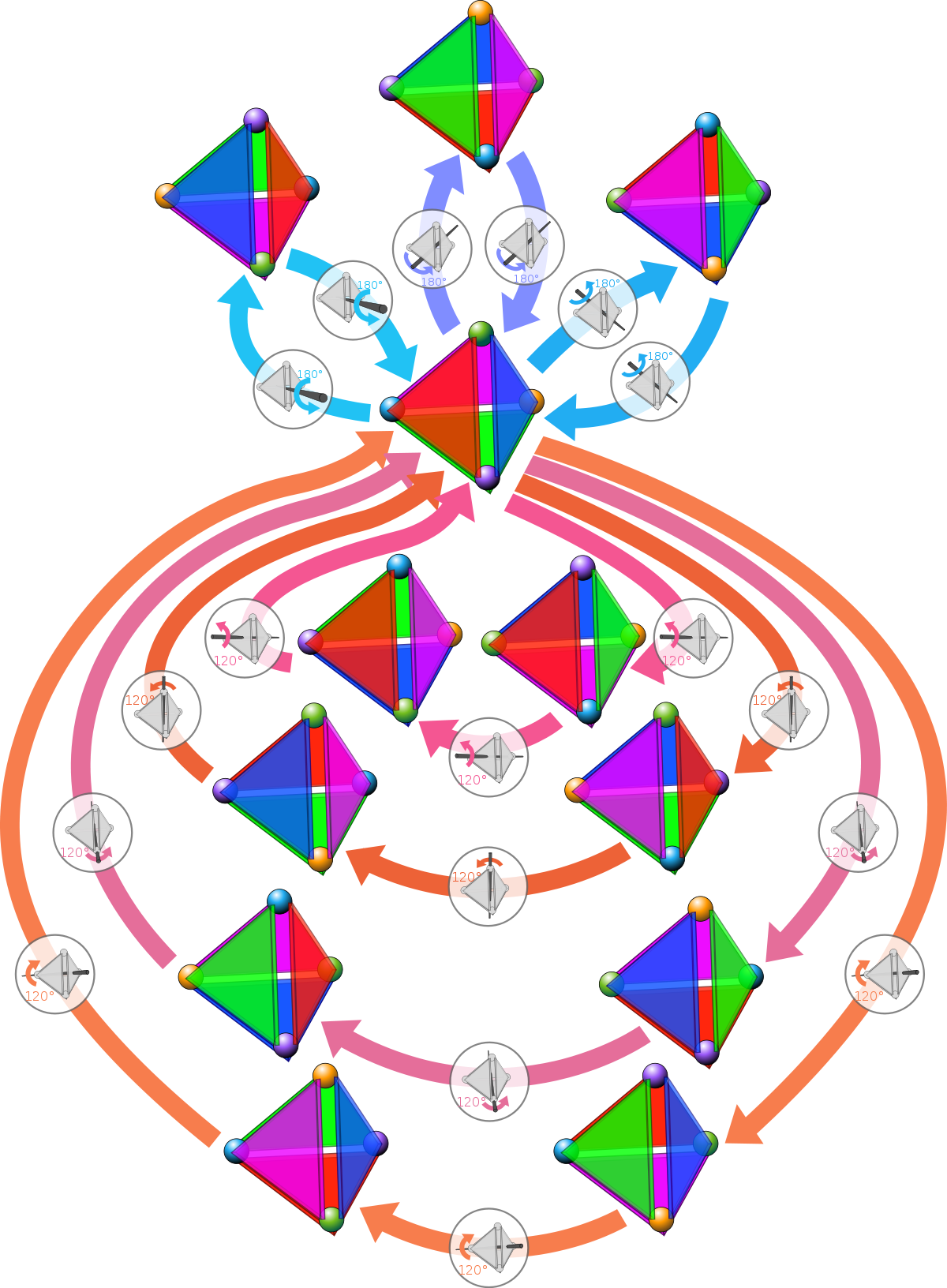
Tout groupe de symétrie dont les éléments ont un point fixe commun, ce qui est vrai pour tous les groupes de symétrie de figures bornées, peut être représenté comme un sous-groupe du groupe orthogonal O(n) en choisissant comme origine un point fixe. Le groupe de symétrie propre est alors un sous-groupe du groupe spécial orthogonal SO(n), c'est pourquoi il est aussi appelé le groupe de rotation de la figure.

Les groupes de symétrie discrets sont de trois sortes :

• les groupes ponctuels de symétrie finis, qui incluent seulement des rotations, des réflexions, des inversions et des rotations impropres - ce sont en fait simplement des sous-groupes finis de O(n),
• les groupes réseaux infinis, qui incluent seulement des translations, et
• les groupes d'espace infinis qui combinent des éléments des deux types précédents, et qui peuvent aussi inclure des transformations supplémentaires comme des vissages ou des réflexions glissées.

Il existe aussi les groupes de symétries continues (en), qui contiennent des rotations d'angles arbitrairement petits ou des translations de distances arbitrairement petites. Le groupe de toutes les symétries d'une sphère O(3) est un exemple de ceci, et en général, de tels groupes de symétries continues sont étudiés comme des groupes de Lie.

À la classification des sous-groupes du groupe euclidien correspond une classification des groupes de symétrie.

On dit que deux figures géométriques ont le même type de symétrie si leurs groupes de symétries respectifs H₁, H₂ sont des sous-groupes conjugués du groupe euclidien E(n), c'est-à-dire s'il existe une isométrie g de Rⁿ telle que H₁=g^-1H₂g. Par exemple :

• deux figures 3D ont une symétrie miroir, mais par rapport à un plan miroir différent
• deux figures 3D ont une symétrie rotationnelle d'ordre 3, mais par rapport à un axe différent
• deux motifs 2D ont une symétrie de translation, chacun dans une direction ; les deux vecteurs de translation ont la même longueur mais une direction différente.

Quelquefois, un concept plus large, le "même type de symétrie" est utilisé, par exemple dans les 17 groupes de papier peint (en)..

Lorsque l'on considère les groupes d'isométrie, on peut se limiter à ceux où pour tous les points, l'ensemble des images sous les isométries est topologiquement fermé. Ceci exclut, par exemple, en dimension 1, le groupe des translations par un nombre rationnel. Une "figure" ayant ce groupe de symétrie est impossible à dessiner et homogène à un niveau de détail arbitraire, sans être réellement homogène.