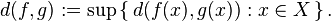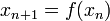Espace complet - Définition
La liste des auteurs de cet article est disponible ici.
Quelques théorèmes
- Un espace métrique (E,d) est complet si et seulement si l'intersection de toute suite décroissante de fermés non vides Fn dont la suite des diamètres tend vers 0 a une intersection non vide (théorème des complets emboîtés).
- Tout espace métrique compact est complet. En fait, un espace métrique est compact si et seulement s’il est complet et précompact.
- Tout sous-espace fermé d'un espace complet est complet, et tout sous-espace complet d'un espace métrique (non nécessairement complet) est fermé.
- Si X est un ensemble et M un espace métrique complet, alors l'ensemble B(X,M) des fonctions bornées de X dans M est un espace métrique complet. On définit la distance dans B(X,M) en termes de distance dans M :
- Si X est un espace topologique et M un espace métrique complet, alors l'ensemble Cb(X,M) des fonctions continues bornées de X dans M est un sous-espace clos de B(X,M) et donc également complet.
- Le théorème de Baire montre que tout espace métrique complet est un espace de Baire.
- Théorème du point fixe : toute application f contractante d'un espace métrique complet dans lui-même admet un unique point fixe qui est limite de toute suite définie de la manière suivante:
-
-
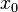
-
- Tout produit fini d'espaces métriques complets est complet pour la distance induite.
- Soit
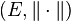
-
- i) E est complet
-
- ii) toute série normalement convergente d'éléments de E est convergente.
Autre acception du terme
Garrett Birkhoff (en) a également introduit le sens suivant de l'épithète "complet" : un ensemble ordonné est dit complet si toute partie admet une borne supérieure (y compris l'ensemble vide, ce qui impose que E ait un minimum). Ceci est équivalent (voir ci-dessous) à ce que toute partie possède une borne inférieure (y compris l'ensemble vide, ce qui impose que E ait un maximum). Par exemple, tout segment est un ensemble ordonné complet. En revanche,


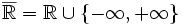
Soit
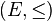
Ainsi, les ensembles ordonnés complets au sens de Birkhoff sont exactement les treillis complets. On dispose donc du théorème de Knaster-Tarski : toute application croissante d'un ensemble ordonné complet dans lui-même possède un point fixe.