Fonction de Green - Définition

Transformée de Fourier

On utilise ci-dessous les notation introduites dans l'article opérateur différentiel.

Opérateur différentiel linéaire à coefficients constants

Rappelons qu'un opérateur différentiel linéaire à coefficients constants d'ordre m s'écrit :

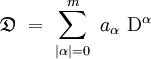
où les a_α sont les coefficents de l'opérateur . Dans toute la suite, on ne considèrera que des opérateurs à coefficients constants : les a_α seront indépendants de x.

Introduction de la transformée de Fourier

Définition

On définit ici la transformée de Fourier de la fonction f(x) de n variables x^k,(k = 1,...,n) par :

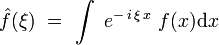
La formule de transformation inverse s'écrit alors :

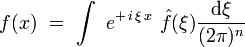
Application aux opérateurs différentiels linéaires à coefficients constants

On obtient la relation :

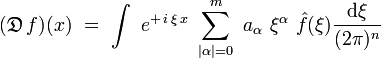
soit encore :

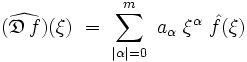
Symbole d'un opérateur différentiel linéaire à coefficients constants

On appelle symbole de l'opérateur différentiel d'ordre m la fonction σ(ξ) des n variables ξ polynomiale en ξ de degré m :

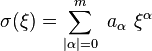
de telle sorte que :

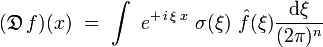
Application aux fonctions de Green

Introduction

Notons la transformée de Fourier de la fonction de Green G(x). L'équation aux dérivées partielles linéaire à coefficients constants définissant les fonctions de Green :

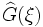
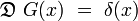
devient, après transformation de Fourier, une équation algébrique :

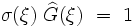
dont la solution est triviale :

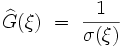
Pour obtenir la fonction de Green originale, il « suffit » alors de calculer la transformée de Fourier inverse :

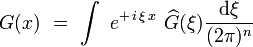
soit explicitement :

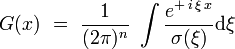
Cette écriture est symbolique, car le symbole σ(ξ) de l'opérateur différentiel d'ordre m étant une fonction polynomiale en ξ de degré m, le théorème fondamental de l'algèbre nous dit que ce polynôme possède m racines complexes, donc que l'intégrande possède à priori m pôles.

Conditions aux limites

Dans les situations physiquement intéressantes, il arrive fréquemment que certains de ces pôles soient situés sur l'axe réel. La transformée de Fourier inverse :

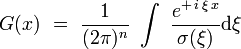
se calcule alors par le théorème des résidus, et le choix du contour fermé et de la prescription de contour des pôles dépend de façon essentielle des conditions aux limites désirées. Il existera donc en général plusieurs fonctions de Green associées à la même équation, qui diffèrent entre-elle par leurs conditions aux limites.

Applications au calcul numérique

Les opérateurs de Green permettent de représenter la solution exacte d'un problème physique (système d'équations aux dérivées partielles) sous forme de convolutions, et s'exprime naturellement dans l'espace de Fourier. Par exemple, en mécanique, les équations de Lippmann-Schwinger permettent d'exprimer le champ de déformation dans un matériau linéaire élastique homogène soumis à une précontrainte au moyen de l'opérateur de Green. Pour les problèmes de conductivité diélectrique, des formulations similaires existent. Ces équations ont non seulement un intérêt théorique mais également pratique.

Les calculs par opérateurs de Green ont de nombreuses applications dans le domaine de l'homogénéisation y compris non-linéaire. Les champs de déformation et de contrainte (ou du champ électrique ou magnétique dans des problèmes de conductivité ou de magnétisme de milieux hétérogènes) sont obtenus numériquement par un algorithme de point de fixe. Les lois constitutives du milieu (traitées dans l'espace réel) et la représentation de la solution par opérateur de Green (traité dans l'espace de Fourier) sont itérés jusqu'à convergence des champs. La majorité du temps de calcul consiste à passer de l'espace réel au domaine de Fourier, à l'aide de transformées de Fourier rapides.