Fonction de Green - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
On appelle fonction de Green en physique ce que les mathématiciens appellent solution élémentaire d'une équation différentielle linéaire à coefficients constants, ou d'une équation aux dérivées partielles linéaire à coefficients constants.
Ces « fonctions » de Green, qui se trouvent être le plus souvent des distributions, ont été introduites par George Green en 1828 pour les besoins de l'électromagnétisme. L'essai de Green restera confidentiel jusqu'à sa republication en trois parties, à partir de 1850. Les fonctions de Green, qui seront dénommées ainsi par Riemann en 1869, seront alors abondamment utilisées, notamment par Neumann en 1877 pour sa théorie du potentiel Newtonien dans un espace à deux dimensions, puis en 1882 par Kirchhoff pour l'équation de propagation des ondes dans un espace à trois dimensions, et enfin par Helmholtz en acoustique.
Elles sont devenues un outil essentiel en théorie quantique des champs après que Feynman les a popularisées en 1948 sous le nom de propagateur dans sa formulation en intégrale de chemin de l'électrodynamique quantique.
Introduction
Position du problème
Soit x = (x1,...,xn) un point de
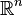

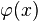
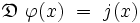
où j(x) est une fonction donnée, appelée source du champ
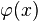
Distribution de Dirac
On note δ(x) la distribution de Dirac. Cette distribution vérifie la propriété fondamentale que, pour toute fonction
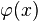
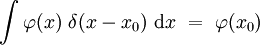
Définition de la fonction de Green
Définition
On appelle fonction de Green G(x) toute solution de l'équation aux dérivées partielles linéaire :
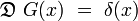
Unicité ?
Il existe en général plusieurs fonctions de Green associées à la même équation. Ces fonctions diffèrent entre-elles par leurs conditions aux limites. C'est pourquoi il est très important de spécifier deux choses pour définir de façon unique une fonction de Green précise :
- l'équation aux dérivées partielles linéaire.
- les conditions aux limites.
Le problème de l'unicité sera précisé plus loin en relation avec la transformée de Fourier.
Intérêt de la fonction de Green
Si la fonction de Green G(x) est connue, alors la solution
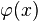
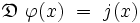
s'écrit simplement sous la forme d'un produit de convolution :
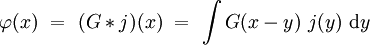
En effet, l'opérateur

![\mathfrak{D} \ \varphi(x) \ = \ \int \left[ \, \mathfrak{D} \ G( x - y ) \, \right] \ j(y) \ \mathrm dy \ = \ \int \delta ( x - y ) \ j(y) \ \mathrm dy \ = \ j(x)](https://static.techno-science.net/illustration/Definitions/autres/b/b0dc3792bd2acd664b01968919e909ed_6f8cbf23bc181f08212e1737a647dee9.png)
Cette équation peut s'interpréter comme la superposition de solutions élémentaires, chaque terme sous l'intégrale représentant la contribution de j(x) entre x et x + dx (on parle encore, en physique, d'interaction à deux corps).
Exemples
Oscillateur harmonique
Considérons l'équation différentielle ordinaire de la fonction de Green de l'oscillateur harmonique à un degré de liberté de pulsation ω0 :
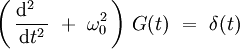
Après transformation de Fourier, cette équation différentielle temporelle devient une équation algébrique pour la pulsation ω, variable conjuguée au temps t :
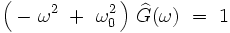
dont la solution est triviale :
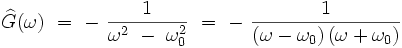
Pour obtenir la fonction de Green temporelle, on doit calculer la transformée de Fourier inverse :
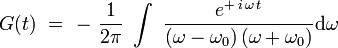
L'intégrande possède deux pôles simples réels, situés respectivement en ω = + ω0 et ω = − ω0 ; on interprète alors l'intégrale comme une intégrale curviligne dans le plan complexe :
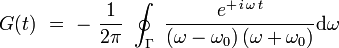
pour laquelle il convient d'abord de fermer le contour Γ. On complète ici l'axe des réels par un demi-cercle centré à l'origine et de rayon R (on prendra la limite
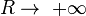
Propagateur retardé
L'hypothèse classique de causalité consiste à postuler a priori que la réponse du système physique suit son excitation, c’est-à-dire ici que le propagateur ne peut être non nul que pour les temps
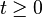
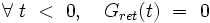
Pour voir dans quel demi-espace du plan complexe il faut situer le demi-cercle, écrivons que :
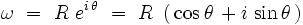
On a alors :
![e^{+ \, i \, \omega \, t} \ = \ \exp \, \left[ \, i \, R \, t \, \left( \, \cos \theta \, + i \, \sin \theta \, \right) \, \right] \ = \ e^{i \, R \, t \, \cos \theta} \ \times \ e^{- \, R \, t \, \sin \theta}](https://static.techno-science.net/illustration/Definitions/autres/9/9cf91941474f242aa33a5169a5b1fb66_97c97ffca18ad47fd7a23f4861a4fc5f.png)
Pour que l'intégrale converge lorsque
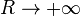
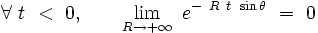
Il faut donc que : sinθ < 0, soit : − π / 2 < θ < 0 : le contour doit être refermé dans le demi-plan complexe inférieur lorsque t < 0.
La fonction de Green devant être identiquement nulle dans ce cas, les deux pôles doivent alors se trouver à l'extérieur de ce contour fermé, c’est-à-dire que les pôles doivent êtres compris comme : ω = ω0 + iε et : ω = − ω0 + iε à la limite où :
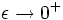
Pour t > 0, le contour doit être refermé dans le demi-plan complexe supérieur.
Le contour fermé contient alors les deux pôles, et le théorème des résidus donne :
![G_{ret}(t) \ = \ - \ \frac{1}{2\pi} \ \times \ 2 \pi i \ \times \ \lim_{\epsilon \to 0^+} \ \left[ \ \left. \frac{e^{+ \, i \, \omega \, t}}{(\omega + \omega_0)} \right|_{\omega = \omega_0 + i \epsilon } \ + \ \left. \frac{e^{+ \, i \, \omega \, t}}{(\omega - \omega_0)} \right|_{\omega = - \omega_0 + i \epsilon } \ \right]](https://static.techno-science.net/illustration/Definitions/autres/e/e290031cb331dea9ebe3565103cb100e_5781a16ee3321f08612e98a34bdbfe54.png)
soit :
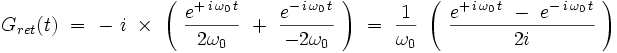
On obtient donc finalement :
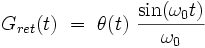
où θ(t) est la distribution de Heaviside.

















































