Groupe de symétrie - Définition

Dimension 1

Les groupes d'isométries en dimension 1 où, pour tous les points, l'ensemble des images sous les isométries est topologiquement fermé sont :

• le groupe trivial C₁
• les groupes de deux éléments engendrés par une symétrie centrale ; ils sont isomorphes au groupe cyclique d'ordre 2, C₂
• les groupes discrets infinis engendrés par une translation ; ils sont isomorphes au groupe cyclique infini, Z
• Les groupes discrets infinis engendrés par une translation et une symétrie centrale ; ils sont isomorphes au groupe diédral généralisé de Z, Dih(Z), ou plus directement au groupe diédral infini D_∞ (qui est un produit semi-direct de Z par C₂ ).
• Le groupe engendré par toutes les translations (isomorphe à R) ; ce groupe ne peut pas être le groupe de symétrie d'un "motif" : il serait homogène, par conséquent il pourrait aussi être réfléchi. Néanmoins, un champ de vecteurs unidimensionnel uniforme a ce groupe de symétrie.
• Le groupe engendré par toutes les translations et réflexions en tous points ; il est isomorphe au groupe diédral généralisé de R, Dih(R).

Dimension 3

À conjugaison près, l'ensemble des groupes ponctuels de symétrie 3D (voir l'article : Groupes ponctuels de symétrie en dimension 3 (en)) est constitué de 7 séries infinies et de 7 autres séparées. En cristallographie, ils sont restreints pour être compatibles avec les symétries discrètes de translation d'un réseau cristallin. Cette restriction cristallographique de la famille infinie de groupes ponctuels généraux a pour résultat 32 groupes ponctuels cristallographiques (27 à partir des 7 séries infinies et 5 des 7 autres).

Les groupes ponctuel de symétrie continus incluent quant à eux :

• la symétrie cylindrique sans une réflexion de plan perpendiculaire à l'axe, ceci s'applique souvent à une bouteille, par exemple.
• la symétrie cylindrique avec une réflexion de plan perpendiculaire à l'axe
• la symétrie sphérique

Pour les objets et les champs scalaires, la symétrie cylindrique implique des plans verticaux de réflexion. Ce n'est pas le cas pour les champs de vecteurs : en coordonnées cylindriques relativement à un certain axe, a une symétrie cylindrique relative à cet axe si et seulement si et A_z ont cette symétrie, i.e., ne dépendent pas de φ. Il existe de plus une réflexion si et seulement si .

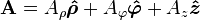
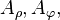
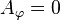
Pour la symétrie sphérique, il n'existe pas de telle distinction, elle implique des plans de réflexion.

Les groupes de symétrie continus sans point fixe incluent ceux avec vissages, tel le groupe d'une hélice infinie.

Dimension 2

À conjugaison près, les groupes de point discrets dans un espace bidimensionnel appartiennent aux classes suivantes :

• les groupes cycliques C₁, C₂, C₃, C₄,... où C_n est constitué de toutes les rotations, autour d'un point fixé, par des multiples de l'angle 360°/n
• les groupes diédraux D₁, D₂, D₃, D₄,... où D_n (d'ordre 2n) est le groupe de symétrie d'un polygone régulier à n côtés. Il est constitué des rotations appartenant à C_n et de n symétries par rapport à des axes qui passent par le centre commun à ces rotations.

C₁ est le groupe trivial contenant seulement l'opération identité, qui apparaît lorsque la figure n'a pas de symétrie du tout, par exemple la lettre F. C₂ est le groupe de symétrie de la lettre Z, C₃ celui d'un triskèle, C₄ d'un svastika et C₅, C₆ etc. sont les groupes de symétrie de figures similaires au svastika avec cinq, six etc. bras à la place de quatre.

D₁ est le groupe à 2 éléments contenant l'opération identité et une réflexion unique, qui apparaît lorsque la figure a seulement un seul axe de symétrie bilatéral, par exemple la lettre A. D₂, qui est isomorphe au groupe de Klein, est le groupe de symétrie d'un rectangle non carré.

Les groupes de symétrie concrets dans chacun de ces cas ont deux degrés de liberté pour le centre de rotation, et dans le cas des groupes diédriques, un de plus pour les positions des miroirs.

Les groupes d'isométrie restants en 2D avec un point fixé, où pour tous les points, l'ensemble des images sous les isométries est topologiquement fermé, sont :

• le groupe spécial orthogonal SO(2) constitué de toutes les rotations autour d'un point fixé ; il est isomorphe au groupe cercle S¹, qui est le groupe multiplicatif des nombres complexes de module 1. C'est le groupe de symétrie propre d'un cercle et l'équivalent continu de C_n. Aucune figure n'a pour groupe de symétrie complet ce groupe cercle, mais pour un champ de vecteurs cela peut arriver (voir le cas 3D ci-dessous),
• le groupe orthogonal O(2) constitué de toutes les rotations autour d'un point fixé et des réflexions d'axe quelconque passant par ce point. C'est le groupe de symétrie d'un cercle. Il est aussi appelé Dih(S¹) car c'est le groupe diédral généralisé de S¹.

Pour les figures non bornées, les groupes d'isométrie supplémentaires peuvent inclure les translations ; ceux qui sont fermés sont :

• les 7 groupes de frise,
• les 17 groupes de papier peint,
• pour chaque groupe de symétrie en 1D, la combinaison de toutes les symétries de ce groupe dans une direction et de toutes les translations dans la direction perpendiculaire,
• idem en ajoutant les réflexions par rapport à un axe dans la première direction.