Opérateur laplacien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Articles d'analyse vectorielle | |

| |
| Objets d'étude | |
| Champ vectoriel | Champ scalaire |
| Équation aux dérivées partielles | |
| de Laplace | de Poisson |
| Opérateurs | |
| Nabla | Gradient |
| Rotationnel | Divergence |
| Laplacien scalaire | Bilaplacien |
| Laplacien vectoriel | D'alembertien |
| Théorèmes | |
| de Green | de Stokes |
| de Helmholtz | de flux-divergence |
| du gradient | du rotationnel |
L'opérateur laplacien, ou simplement le laplacien, est l'opérateur différentiel défini par l'application de l'opérateur gradient suivie de l'application de l'opérateur divergence. Il apparaît dans la formulation mathématique de nombreuses disciplines théoriques, comme la géophysique, l'électrostatique, la thermodynamique, la mécanique classique et quantique. On le retrouve systématiquement dans les expressions de l'équation de Laplace, de l'équation de Poisson et de l'équation de la chaleur.
Symbolisé par la lettre grecque delta, il correspond donc à l'opérateur nabla appliqué deux fois à la fonction considérée, d'où les identités :
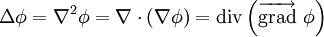
Il s'applique aux champs scalaires. L'opérateur laplacien vectoriel, lui, s'applique aux champs vectoriels. Le laplacien admet une généralisation aux espaces non-euclidiens suffisamment lisses, appelé opérateur de Laplace-Beltrami. L'opérateur laplacien appliqué deux fois est appelé bilaplacien.
De manière plus générale, la définition du laplacien par la divergence du gradient (celle-ci étant prise sur l'indice tensoriel créé par le gradient) est valable pour un champ tensoriel quelconque a. Le laplacien
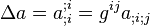
a le même nombre d'indices que a.
Pour un champ scalaire, on a :
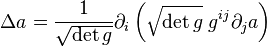
Cette formule permet, une fois établi le tenseur métrique g, de calculer facilement le laplacien dans un système de coordonnées quelconque.
Expression dans différents systèmes de coordonnées
Coordonnées cartésiennes
- En coordonnées cartésiennes bidimensionnelles, le laplacien est :
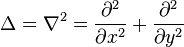
- En coordonnées cartésiennes tridimensionnelles :
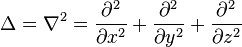
- En coordonnées cartésiennes dans

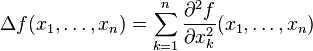
Coordonnées cylindriques
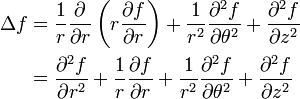
Coordonnées sphériques
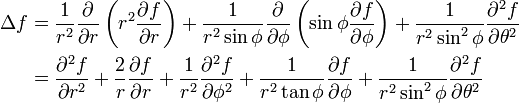
Fonction harmonique
Une fonction
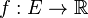
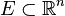
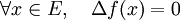
Propriétés
- L'opérateur laplacien est linéaire :
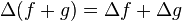
- L'opérateur laplacien vérifie la règle de Leibniz pour un opérateur différentiel d'ordre deux :
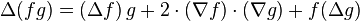
- L'opérateur laplacien est un opérateur négatif, au sens où, pour toute fonction φ lisse à support compact, on a :
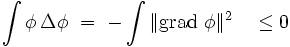
Interprétation
Le raisonnement se limitera au cas du plan. La dérivée d'une fonction en un point situé sur une droite se définit comme la limite du rapport des variations autour de ce point de la fonction et de la variable lorsque cette dernière variation tend vers zéro. En calcul numérique, une approximation de cette dérivée est donc obtenue pour un pas h en utilisant des différences finies :
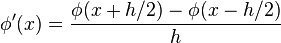
La dérivée seconde s'exprime par
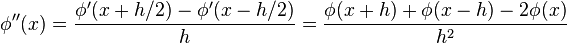
Cette quantité, qui tend vers le Laplacien lorsque h tend vers 0, est proportionnelle à la différence entre la somme des valeurs extrêmes et la valeur centrale. La propriété se généralise à un nombre quelconque de variables.
Approche géométrique
Il est indispensable de bien dégager une interprétation physique simple pour le laplacien, autrement dit de se demander quelle est la signification physique de la quantité ∇2ϕ, où ϕ est une grandeur physique quelconque. En particulier, ϕ peut être le potentiel gravifique V ou le potentiel de pesanteur U, mais ϕ peut aussi désigner une quantité plus compliquée qu'une simple grandeur scalaire, par exemple un vecteur ou un tenseur. Le laplacien étant un opérateur scalaire, on peut donc établir sa signification physique dans un système de coordonnées au choix. Pour des raisons de simplicité, nous utilisons ici des coordonnées cartésiennes Ox,Oy,Oz, dans lesquelles ∇2 s'exprime par
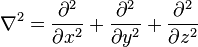
Supposons qu'en un point O quelconque, pris comme origine de ce système d'axes Oxyz, le champ ϕ prenne la valeur ϕ0. Considérons un cube élémentaire de côté a, dont les arêtes sont parallèles aux axes de coordonnées et dont le centre se confond avec l'origine O. La valeur moyenne de ϕ dans ce cube élémentaire, autrement dit la valeur moyenne de ϕ au voisinage du point O, est fournie par l'expression
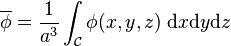
où les trois intégrations portent chacune sur le cube C = [−a⁄2, a⁄2]3.
En un point P(x,y,z) arbitraire au voisinage de O(0,0,0) développons ϕ en série de Taylor-Maclaurin. On a ainsi :
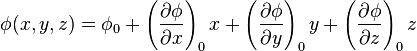
![+ \frac12 \left[ \left(\frac{\partial^2\phi}{\partial x^2}\right)_0 x^2 + \left(\frac{\partial^2\phi}{\partial y^2}\right)_0 y^2 + \left(\frac{\partial^2\phi}{\partial z^2}\right)_0 z^2 \right]](https://static.techno-science.net/illustration/Definitions/autres/f/ffc41d93bca9391510a305f391c0e897_dad93556e16806d179c975046471724c.png)
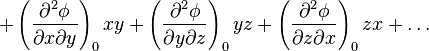
D'une part, les fonctions impaires dans cette expression fournissent, par intégration de −a⁄2 à a⁄2, une contribution nulle à ϕ. Par exemple,
![\int_\mathcal C x\;\mathrm dx \mathrm dy \mathrm dz = \left[ \frac{\left(\frac a2\right)^2}2 - \frac{\left(\frac{-a}2\right)^2}2\right] \left[\frac a2 - \frac{-a}2\right] \left[\frac a2 - \frac{-a}2\right] = [0] [a] [a] = 0](https://static.techno-science.net/illustration/Definitions/autres/f/f979ed32b72b468e42339fa9882cd09a_5eb6beaf74c39c184dd7601f6cde42f4.png)
D'autre part, les fonctions paires fournissent chacune une contribution de a5/12. Par exemple,
![\int_\mathcal C x^2\;\mathrm dx \mathrm dy \mathrm dz = \left[\frac{\left(\frac a2\right)^3}3 - \frac{\left(\frac{-a}2\right)^3}3\right] \left[\frac a2 - \frac{-a}2\right] \left[\frac a2 - \frac{-a}2\right] = \frac{a^5}{12 }](https://static.techno-science.net/illustration/Definitions/autres/b/b733bb8903625133c3a4566ed71e6856_0535049ed29445d0cb72d4ca10ede2a3.png)
On en déduit que
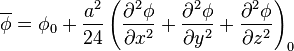
ou encore
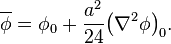
Comme le point O a été choisi arbitrairement, on peut l'assimiler au point courant P et laisser tomber l'indice « 0 ». On obtient donc l'expression suivante, dont l'interprétation est immédiate :
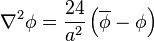
c'est-à-dire la quantité ∇2ϕ est proportionnelle à la différence ϕ–ϕ. La constante de proportionnalité vaut 24/a2 en axes cartésiens. En d'autres termes, la quantité ∇2ϕ est une mesure de la différence entre la valeur de ϕ en un point quelconque P et la valeur moyenne ϕ au voisinage du point P. En particulier, les solutions de l'équation de Laplace, que l'on appelle des fonctions harmoniques, ont la propriété d'être des fonctions moyennes (ou des « fonctions de classe moyenne » dans le jargon mathématique).
Remarque : Le laplacien d'une fonction peut aussi être interprété comme la courbure moyenne locale de la fonction, que l'on visualise aisément pour une fonction à une seule variable f(x). On vérifiera aisément que le raisonnement proposé ici pour le laplacien s'applique à une fonction f(x) et à sa dérivée seconde. La dérivée seconde (ou courbure) représente ainsi la déviation locale de la moyenne par rapport à la valeur au point considéré.

















































