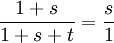Heptagone - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Construction par neusis
Une construction par neusis ou par inclinaison est un procédé de construction utilisant une règle graduée et consistant à construire un segment de longueur donnée dont les extrémités se trouvent sur deux courbes données. Il s'agit ici de construire un angle de
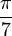
Une construction préliminaire
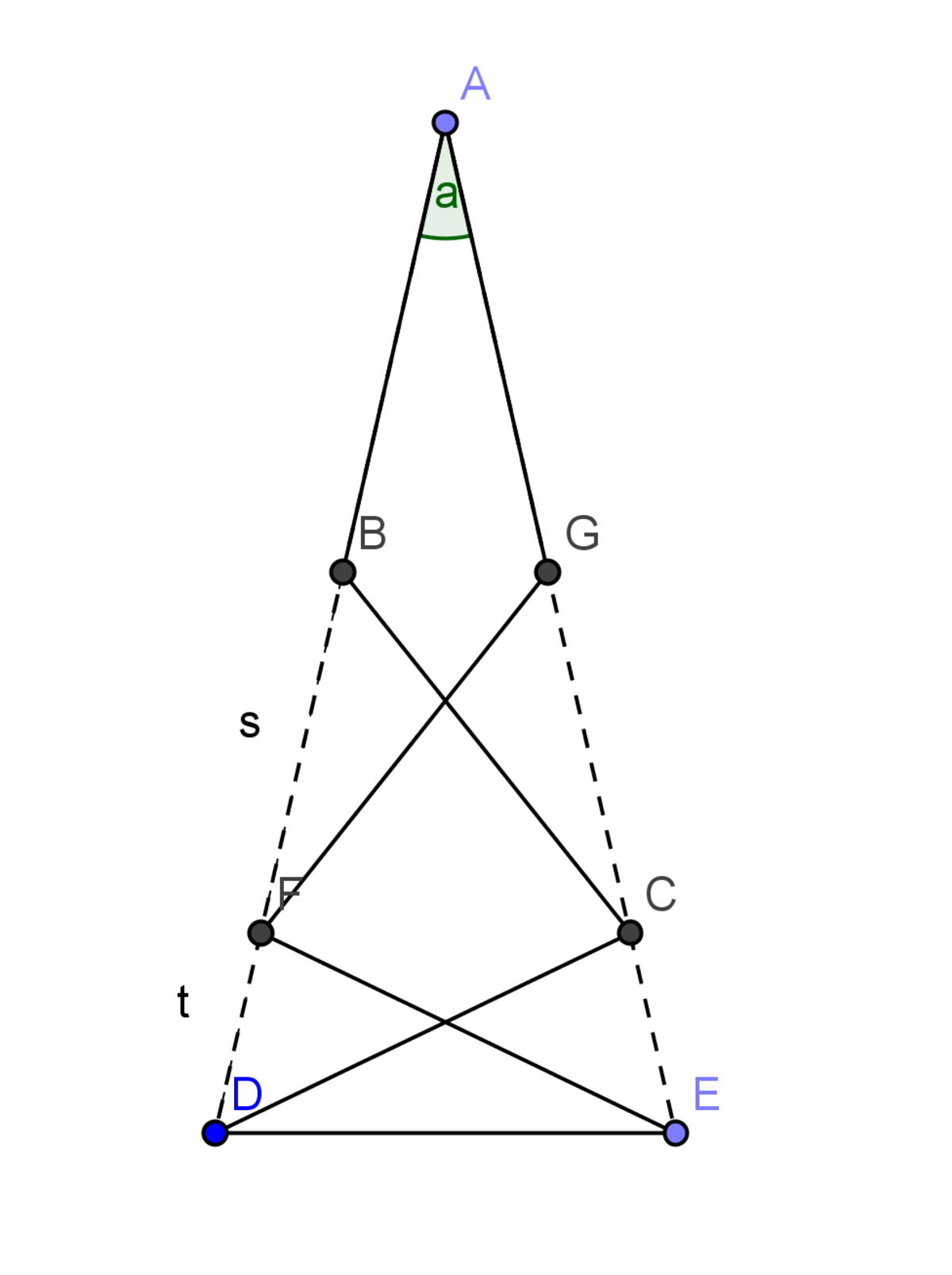
Dans la figure jointe, ABCDEFGA est un polygone où tous les segments sont de longueur 1. ABFD sont alignés et AGCE aussi.
L'angle DAE vaut
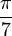
- Si on note cet angle a, alors le triangle ABC étant isocèle, l'angle CBD vaut 2a.
- Le triangle BCD étant isocèle, la somme des angles DCE et BCA vaut 4a, comme BCA vaut a, l'angle DCE vaut 3a
- Le triangle CDE étant isocèle, l'angle AED vaut 3a
- Le triangle ADE étant isocèle, la somme des angles vaut 7a donc
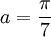
La longueur BE vaut
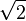
- On note s et t les longueurs BF et FD.
- Le triangle FDE étant isocèle, 2cos(EDF) = t
- Les droites (FC) et (DE) étant parallèles, l'angle ACF vaut 3a. Comme l'angle ACB vaut a, l'angle BCF vaut 3a-a = 2a. Le triangle BFC est donc isocèle et FC = FB = s
- Le même parallélisme permet de dire, d'après le théorème de Thales, que
-
- qui par produit en croix et simplification donne s2 + st = 1
- Le théorème d'Al-Kashi dans le triangle BDE donne alors
- BE2 = BD2 + DE2 − 2.BD.DE.cos(EDF) = 1 + (s + t)2 − t(s + t) = 1 + s2 + st = 2
La construction par neusis
Il s'agit de construire un point A sur la médiatrice d'un segment [DE] et un point B sur le segment [AD] tels que AB = 1 et BE =
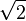
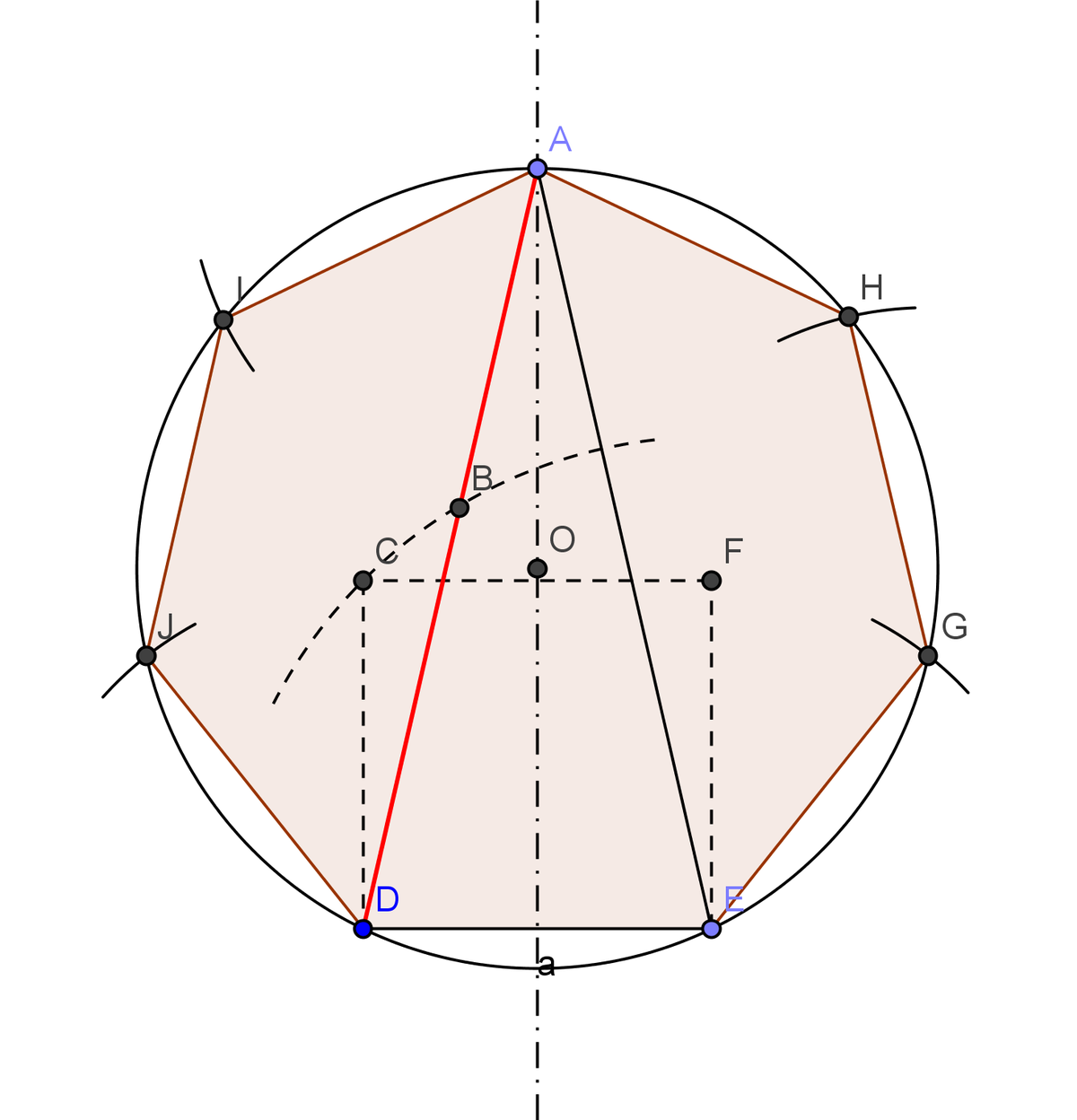
- On construit un carré CDEF de côté 1, on trace la médiatrice (d) de [DE] et le cercle de centre E et de rayon EC
- On place l'origine de la règle sur la médiatrice, la règle s'appuie sur le point D, on fait glisser l'origine de la règle sur la médiatrice jusqu'à ce que le cercle (C) traverse la règle à la graduation 1. On obtient alors les points B et A
- On construit le cercle circonscrit aux points ADE qui se trouve être aussi le cercle circonscrit de l'heptagone de base DE qu'il suffit de construire.
Heptagone régulier dans la vie courante
- La pièce de 20 centimes d'euros est découpée sous forme d'un heptagone régulier.
- Les pièces britanniques de 20 et de 50 pence sont également heptagonales.