Heptagone - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un heptagone est un polygone à sept sommets et sept côtés.
Un heptagone régulier est un heptagone dans lequel tous les côtés sont égaux et tous les angles sont égaux. Les angles sont alors tous égaux à
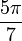
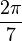
L'aire A d'un heptagone régulier est déterminée par la formule suivante où c représente la longueur d'un côté :
L'heptagone régulier est le plus petit des polygônes réguliers non constructible à la règle et au compas car 7 est un nombre premier qui n'est pas de Fermat (théorème de Gauss-Wantzel) .
Il est cependant possible de réaliser une construction à la règle et au compas si on s'aide d'autres outils géométriques ou si la règle peut être graduée. Il est aussi possible d'en tracer une version approchée, aux erreurs faibles, avec le compas et la règle.
Non constructiblité
L'heptagone régulier n'est pas constructible car 7 n'est pas un nombre de Fermat. On peut aussi démontrer cette propriété de non-constructiblité sans faire appel au nombre de Fermat , en faisant seulement appel au théorème de Wantzel
Si l'heptagone était constructible alors

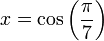
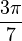
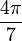
Les développements
- cos(4a) = 8cos4(a) − 8cos2(a) + 1
- cos(3a) = 4cos3(a) − 3cos(a)
transforment [1] en
- 8x4 − 8x2 + 1 = − 4x3 + 3x
Le passage de tout dans un membre et une factorisation par x + 1 conduit à
- (x + 1)(8x3 − 4x2 − 4x + 1) = 0
Le réel x est donc racine de 8x3 − 4x2 − 4x + 1 irréductible sur


Constructions approchées
À l'aide d'un triangle équilatéral
La recherche approchée de la solution de l'équation 8x3 − 4x2 − 4x + 1 = 0 comprise entre

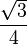

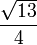
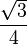
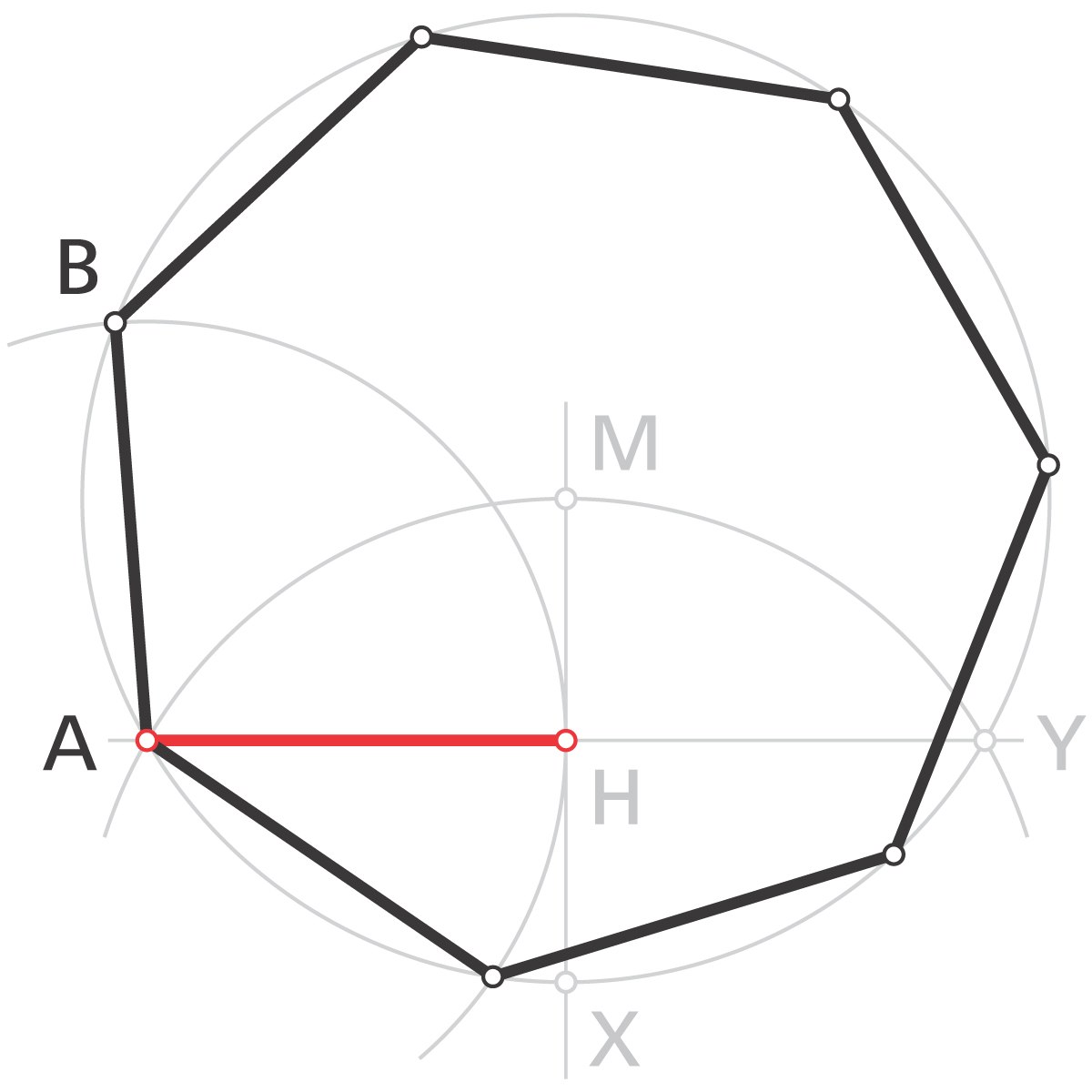
D'où la construction suivante :
- Tracer un cercle de rayon 1 et de centre M.
- Prendre un point X sur le cercle. Le cercle de centre X et de rayon XM rencontre le cercle précédent en A et Y
- Les droites (AY) et (MX) se coupent en H.
- La longueur AH est une bonne approximation du côté de l'heptagone inscrit dans ce même cercle.
Par cette méthode l'angle au centre est d'environ 51,32 degrés au lieu des 51,43 (environ) attendu, soit une erreur relative de 2,15 pour mille
Construction à l'aide d'un découpage de segment
En s'inspirant de la construction de l'enneagone, on peut tracer une construction approchée d'un heptagone régulier, à la règle et au compas.
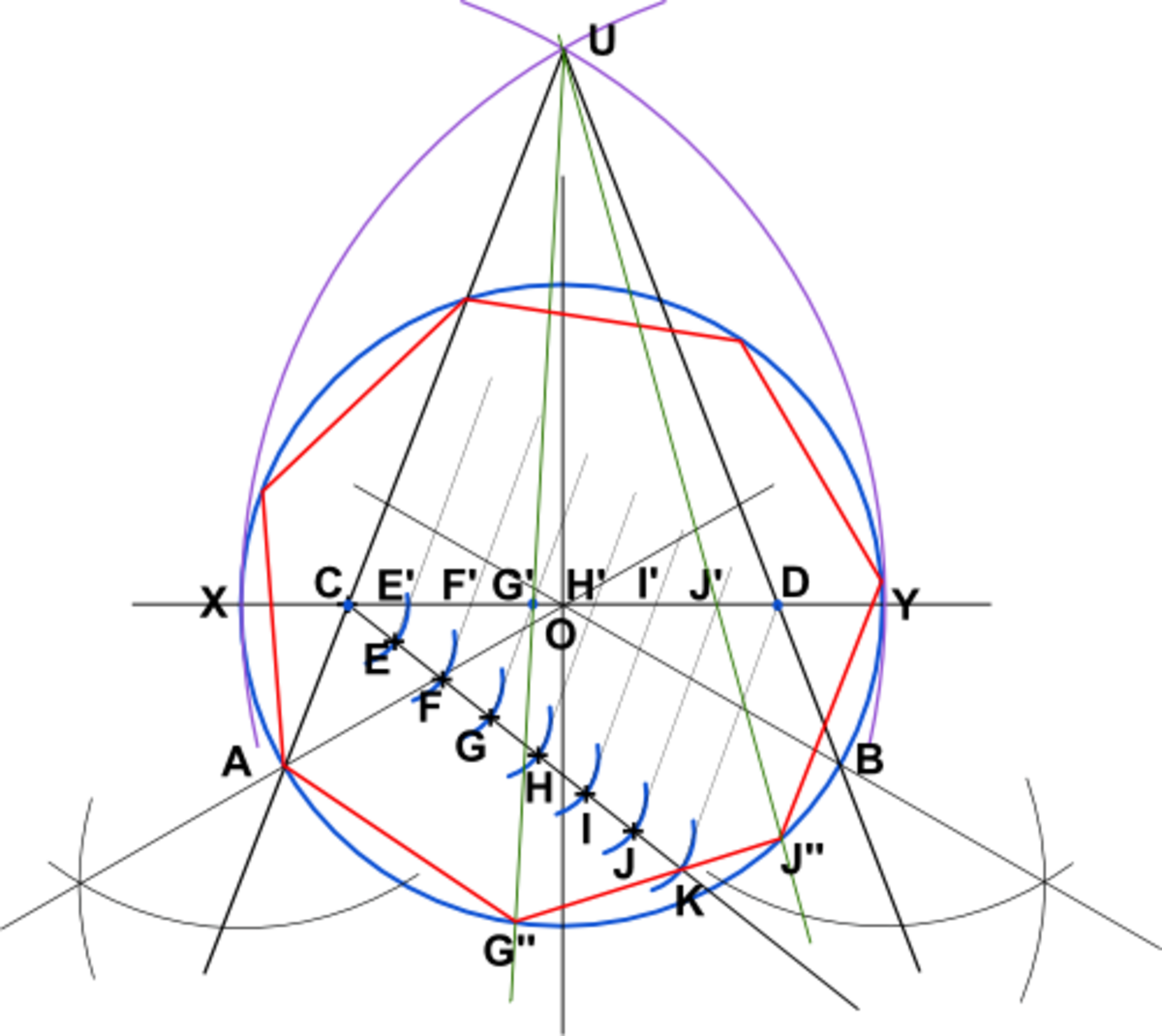
- Tracer le cercle de centre O de rayon OX
- Place, sur le cercle deux points A et B tels que l'angle AÔB = 120°.
- Tracer l'arc de cercle de rayon XY et de centre X
- Tracer l'arc de cercle de rayon YX et de centre Y
- Ces arcs se coupent en U
- Tracer les droites (UA) et (UB). Elles coupent le diamètre (XY) en C et D
- A partir de C, sur une droite quelconque, porter avec un compas sept segments égaux CE = EF = FG = GH = HI = IJ = JK
- Tracer la droite (KD) et mener par G une parallèle à celle-ci (au moyen de la règle et du compas), qui coupe (XY) en G’. Éventuellement tracer la parallèle à (KD) passant par J qui coupe (XY) en J’.
- Tracer la droite (UG').Elle coupe le cercle en G’’.
- Reportez au compas tout le long du cercle la longueur AG’’, on trouve alors les sept sommets de l'heptagone régulier inscrit dans le cercle.
Remarque : pour faire un heptagone comprenant le point B, il aurait fallu prendre les points H’’ ou E’’. De plus, en utilisant le point F’’, en reportant AF’’, on obtient un polygone à 21 sommets.
Par cette construction, l'angle au centre AOG’’est d'environ 51,327, soit une erreur relative de 1,98 pour mille équivalente à l'erreur obtenue par la méthode précédente.
Cette méthode permet de faire n'importe quel polygone régulier. Il suffit de sectionner le segment CD en autant de secteurs identiques qu'il y a de côtés souhaités pour le polygone. Ensuite, on prend le troisième point en partant de C (G’), on trace le segment qui le relie à U et on obtient G’’ à l'intersection entre le cercle et ce segment (dans le demi-plan inférieur à XY). L'erreur commise sur l'angle au centre pour cette méthode varie de 1,98 pour mille à 11,7 pour mille selon le nombre de côtés.

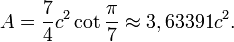
![\cos\left(\frac{4\pi}{7}\right)=-\cos\left(\frac{3\pi}{7}\right) \quad[1]](https://static.techno-science.net/illustration/Definitions/autres/f/ff1f84b9578a92c5db7ba54a608b9b87_9cba4c44634ed3d2320a95e928712990.png)