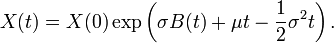Lemme d'Itô - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le lemme d'Itô, ou encore formule d'Itô est l'un des principaux résultats de la théorie du calcul stochastique. Ce lemme offre un moyen de manipuler le mouvement brownien ou les solutions d'équations différentielles stochastiques (EDS).
Énoncé
Si

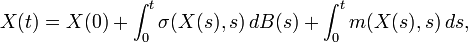
ou de
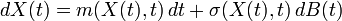
où
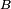
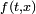
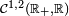
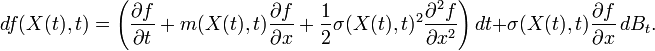
Dans le cas d'un mouvement brownien
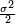

Histoire
La formule d'Itô a été démontrée pour la première fois par le mathématicien japonais Kiyoshi Itô dans les années 1940.
Le mathématicien Wolfgang Doeblin avait de son côté ébauché une théorie similaire avant de se suicider à la défaite de son bataillon en juin 1940. Ses travaux furent envoyés dans un pli cacheté à l'Académie des sciences qui ne fut ouvert qu'en 2000.
Applications
- La formule d'Itô est l'une des pierres angulaires du calcul stochastique, et est utilisée dans de très nombreux domaines: mathématiques appliquées, physique, finance, biologie, Mécanique quantique, traitement du signal, etc..
En calcul stochastique,
- Elle permet de faire le lien entre les solutions d'EDS et des opérateurs différentiels du second ordre, et donc entre la théorie des probabilités et celle des équations aux dérivées partielles.
- Elle permet d'affirmer l'existence de solutions d'EDS sous des conditions (très) faibles de régularité sur les coefficients.
Un exemple : le modèle Black-Scholes
Le mouvement brownien geometrique est souvent utilisé en finance comme le plus simple modèle d'évolution de cours de bourse. Il s'agit de la solution de l'équation différentielle stochastique :
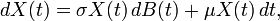
où
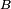
Si
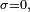
En posant
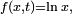
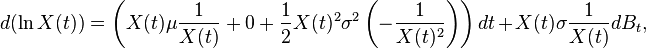
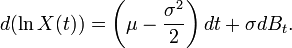
On peut alors intégrer et il en découle que :