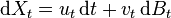Calcul stochastique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le calcul stochastique est l’étude des phénomènes aléatoires dépendant du temps. À ce titre, il est une extension de la théorie des probabilités.
Applications
Le domaine d’application du calcul stochastique comprend :
- la mécanique quantique,
- le traitement du signal,
- la chimie,
- les mathématiques financières,
- la météorologie,
- et même la musique.
Filtrations
Une filtration Ft,
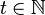
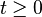
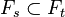
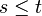
Espérance conditionnelle selon une filtration
Processus aléatoires
Un processus aléatoire X est une famille de variables aléatoires indexée par un sous-ensemble de

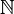

Autre prescription
Il existe une autre prescription notable pour définir une intégrale stochastique, c'est la prescription de Stratonovich. L'intégrale de Stratonovich est définie comme la limite des sommes discrètes
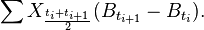
La différence notable avec la prescription d'Itô est que la quantité
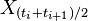
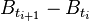
![E\left[\int_{a}^{b} X_t\, \mathrm dB_t\right]\neq 0](https://static.techno-science.net/illustration/Definitions/autres/2/23ca56be5f13116dd3734d8cc620ebd2_4d87636db6dc1327cd6c31bc8921450c.png)
ce qui complique, de ce point de vue, certains calculs. Cependant l'utilisation de la prescription de Stratonovich ne choisit pas une direction du temps privilégiée contrairement à celle d'Itô ce qui implique que les processus stochastiques définis par l'intégrale de Stratonovich satisfont des équations différentielles stochastiques invariantes par renversement du temps. Pour cette raison, cette prescription est souvent utilisée en physique statistique.
Il faut noter cependant qu'il est possible de passer de l'une à l'autre des prescriptions en effectuant des changements de variables simples ce qui les rend équivalentes. Le choix de prescription est donc une question de convenance.
Processus d'Itō
Le processus d'Itō, d'après le nom de son inventeur Kiyoshi Itō, traite des opérations mathématiques dans un processus stochastique. Le plus important est l'intégrale stochastique d'Itō.
Intégrale d'Itô
Avant le calcul, indiquons que :
- Les majuscules telles que X notent les variables aléatoires.
- Les majuscules avec en indice un t (par exemple Bt) notent un processus stochastique qui est une famille de variables aléatoires indexée par t.
- Un petit d à gauche d'un processus (par exemple dBt) signifie un changement infinitésimal dans le processus aléatoire qui est une variable aléatoire.
L'intégrale stochastique d'un processus Xt par rapport à un processus Bt est décrite par l'intégrale :
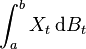
et est définie comme la limite en moyenne quadratique des sommes correspondantes de la forme :
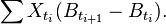
Un point essentiel lié à cette intégrale est le lemme d'Itô.
La somme comme le produit de variables aléatoires est définie dans la théorie des probabilités. La somme implique une convolution de la fonction de densité des probabilités, et la multiplication est une addition répétée.
Définition d'un processus d'Itô
Une fois précisée la définition choisie pour une intégrale stochastique, on définit alors un processus d'Itô comme étant une processus stochastique Xt de la forme
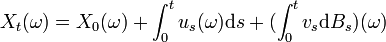
avec u et v deux fonctions aléatoires satisfaisant quelques hypothèses techniques d'adaptation au processus Bt et ω est une réalisation dans l'espace de probabilité sous-jacent.
Dans le formalisme du calcul différentiel avec la prescription d'Itô on note de façon équivalente la relation précédente comme