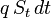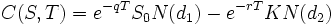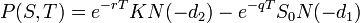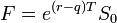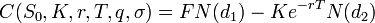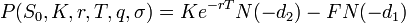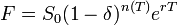Modèle Black-Scholes - Définition
Le modèle de Black-Scholes (du nom de Fischer Black et Myron Scholes) d'évaluation d'option est un modèle utilisé en mathématiques financières afin d'estimer en théorie la valeur d'une option financière, du type option européenne.
Importance historique et économique
Il fut publié en 1973, et constituait le prolongement de travaux réalisés par Paul Samuelson et Robert Merton. Le mathématicien français Louis Bachelier avait inauguré l'étude du sujet en 1900. L'intuition fondamentale de Black et Scholes fut de mettre en rapport le prix implicite de l'option et les variations de prix de l'actif sous-jacent. Leur découverte eut très rapidement une influence considérable, et des déclinaisons de leur modèle sont utilisées dans tous les compartiments des marchés financiers. Dès 1977, Oldrich Vasicek s'en inspirait pour fonder la théorie moderne des taux d'intérêt.
Merton et Scholes reçurent en 1997 le "prix Nobel d'économie" pour leurs travaux (Fisher Black était, lui, malheureusement mort en 1995).
Formule de Black-Scholes
La formule de Black-Scholes permet de calculer la valeur théorique d'une option à partir des cinq données suivantes :
-
-
-
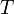
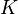
- le taux d'intérêt sans risque
-
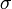
Le prix théorique d'une option d'achat (call), qui donne le droit mais pas l'obligation d'acheter l'actif S à la valeur K à la date T, est caractérisé par son pay off :
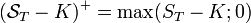
Le prix de l'option est donné par l'espérance sous probabilité risque neutre du pay off terminal actualisé
![C = E[Payoff \times e^{-rT}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0fd0f6f99550f8b42573e6544d751e7c_205fa32e5ac832cf2bb7046585f600f3.png)
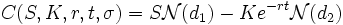
De même,le prix théorique d'une option de vente (put), de pay off
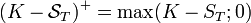
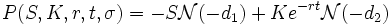
avec
-
-
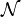
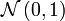
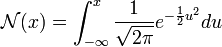
![d_1 = \frac{1}{\sigma\sqrt{t}} \left[ \ln \left( \frac{S}{K} \right) + \left( r + \frac{1}{2}\sigma^2 \right)t \right]](https://static.techno-science.net/illustration/Definitions/autres/4/4ad9f2c6ddc286d53d764570663c7ca6_39dc85e0595ee3940d2c08a930a9fa85.png)
-
![d_1 = \frac{1}{\sigma\sqrt{t}} \left[ \ln \left( \frac{S}{K} \right) + \left( r + \frac{1}{2}\sigma^2 \right)t \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4ad9f2c6ddc286d53d764570663c7ca6_39dc85e0595ee3940d2c08a930a9fa85.png)
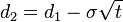
La formule de Black-Scholes repose sur l'hypothèse que les rendements de l'actif sous-jacent sont gaussiens, ou de manière équivalente que la valeur de l'actif suit une diffusion brownienne géométrique.
Les quatre premières données sont évidentes, seule la volatilité
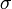
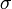
On peut également appliquer la formule à l'inverse. Étant donné le prix de l'option qui est coté dans les marchés, quelle valeur de
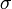
Modèle de Black-Scholes
La formule de Black-Scholes peut être démontrée rigoureusement si un certain nombre de conditions sont établies. On parle alors de modèle de Black-Scholes, ou on dit qu'on est dans le cas Black-Scholes. Les marchés financiers correspondent assez bien à ce modèle, mais pas exactement bien sûr et, en particulier, contrairement à l'hypothèse centrale du modèle, le temps n'y est pas continu. Il y a donc un certain écart entre ce modèle et la réalité, qui peut devenir important quand les marchés sont agités avec de fréquentes discontinuités de cours.
Les conditions du modèle sont les suivantes :
- le prix du sous-jacent suit un mouvement brownien géométrique ;
- la volatilité est connue à l'avance et est constante ;
- il est possible d'acheter et de vendre le sous-jacent à tout moment et sans frais ;
- les ventes à découvert sont autorisées (où on emprunte une certaine quantité du sous-jacent pour la vendre) ;
- il n'y a pas de dividende ;
- le taux d'intérêt est connu à l'avance et est constant ;
- l'exercice de l'option ne peut se faire qu'à la date d'échéance, pas avant (option à exercice européen, dite option européenne).
Le modèle de Black et Scholes en pratique
La thèse fondamentale du modèle de Black et Scholes était que le prix de l'option d'achat est indiqué implicitement si le sous-jacent est échangé sur les marchés.
L'utilisation du modèle et de la formule Black-Scholes est très répandue sur les marchés financiers, à tel point que certaines cotations se donnent en niveau de volatilité plutôt qu'en prix absolu. En effet, les autres paramètres du modèle (durée à l'échéance, prix d'exercice, taux d'intérêt sans risque et prix du sous-jacent) sont facilement observables sur les marchés.
Cependant, le modèle de Black et Scholes ne permet pas de modéliser précisément le monde réel. L'expérience montre qu'en réalité la volatilité dépend du prix d'exercice et de la maturité.
En pratique, la surface de volatilité (la volatilité implicite en fonction du prix d'exercice et de la maturité) n'est pas plate. Souvent, pour une maturité donnée, la volatilité implicite par rapport au prix d'exercice a une forme de sourire (appelé le smile de volatilité) : à la monnaie, la volatilité implicite est la plus basse et plus on s'éloigne de la monnaie, plus elle est élevée. On constate par ailleurs que le smile n'est souvent pas symétrique sur le marché des actions : plus haut du coté put que du coté call. Cela est dû au fait que les acteurs de marché sont plus sensibles au risque de baisse qu'au risque de hausse de l'action.
Pour un prix d'exercice donné, la différence entre la volatilité implicite observée et celle à la monnaie s'appelle le skew.
La surface de volatilité d’un sous-jacent évolue également dans le temps. Les acteurs du marché la réévaluent sans cesse, modifiant leur anticipation de la probabilité, pour chaque prix d'exercice et maturité, qu'une option ne finisse dans la monnaie.
Extensions de la formule
La formule de prix d'option ci-dessus est employée pour l'évaluation d'options européennes sur les actions ne payant pas de dividendes. Le modèle Black-Scholes peut être facilement étendu aux options sur des instruments payant des dividendes. Pour les options sur des indices (tels que le FTSE ou le CAC 40) où chacune des entreprises entrant dans son calcul peut payer un dividende une ou deux fois par an, il est raisonnable de supposer que les dividendes sont payés sans interruption.
Le paiement des dividendes au cours d'une période de temps
![\left[ t , t+\delta t \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/ace6d105706ba15f858414cd2e861df1_4dd051fd5b923c33f18bb06d7f9513ac.png)
pour un q constant. Sous cette formulation le prix arbitrage-libre selon le modèle Black-Scholes peut être montré comme étant :
où maintenant :
est le prix modifié de l'avant qui se produit aux termes d1 and d2. Cette formule est generalement connue comme Black-Scholes-Merton.
Exactement la même formule est employée pour évaluer des options sur des taux de devises étrangères, sauf que maintenant q prend le rôle du taux d'intérêt sans-risque étranger et S le taux de change immédiat. C'est le modèle de Garman-Kohlhagen (1983).
C’est également possible d’étendre le cadre Black-Scholes aux options sur des instruments payant des dividendes discrets. C'est utile quand l'option est basée sur des actions simples.
Un modèle typique doit supposer qu'une proportion δ du prix (cours) d'actions ait payé comme dividende aux dates prédéterminées T1,T2....
Le prix des actions est alors modelé comme:
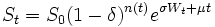
où n(t ) est le nombre de dividendes qui ont été payés au temps t .
Le prix d'une option d'achat sur des telles actions est encore:
où maintenant :
est le prix en avance des actions payant du dividende.
Il est plus difficile d’évaluer des options américaines, et un choix des modèles est (par exemple) Whaley (modèle binomial d'options).