Lois du mouvement de Newton - Définition

Introduction

Les deux premières lois de Newton en latin dans l'édition originale du Principia Mathematica de 1687.

Les lois du mouvement de Newton sont en fait des principes à la base de la grande théorie de Newton concernant le mouvement des corps, théorie que l'on nomme aujourd'hui Mécanique newtonienne ou encore Mécanique classique. À ces lois générales du mouvement fondées en particulier sur le principe de relativité des mouvements, Newton a ajouté la loi de la gravitation universelle permettant d'interpréter aussi bien la chute des corps que le mouvement de la Lune autour de la Terre.

Première loi de Newton ou principe de l'inertie

Énoncé

L'énoncé original de la première loi du mouvement est le suivant :

« Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n'agisse sur lui, et ne le contraigne à changer d'état. »

Dans la formulation moderne de la loi, on parle de mouvement rectiligne uniforme, et on remplace la notion de force (unique) par celle, plus générale, de résultante des forces appliquées sur le corps. Autrement dit, s'il n'y a pas de force qui s'exerce sur un corps (corps isolé), ou si la somme des forces (ou force résultante) s'exerçant sur lui est égale au vecteur nul (corps pseudo-isolé), la direction et la norme de sa vitesse ne changent pas ou, ce qui revient au même, son accélération est nulle. Cette première loi infirme la conception héritée d'Aristote, selon laquelle pour maintenir la vitesse d'un mobile constante, il était nécessaire de lui appliquer une force.

Bien que Newton ne l'ait pas précisé dans son ouvrage, cette loi n'est valable que dans un référentiel galiléen. La première loi de Newton peut donc être reformulée dans un langage plus moderne :

« Dans un référentiel galiléen, le vecteur vitesse du centre d'inertie d'un système est constant si et seulement si la somme des vecteurs forces qui s'exercent sur le système est un vecteur nul. »

Problème du référentiel galiléen

La définition d'un référentiel galiléen apparaît fondamentale et est souvent formulée ainsi :

« Un référentiel galiléen est un référentiel dans lequel la première loi de Newton est vérifiée. »

Ainsi la première loi de Newton ne s'applique que dans un référentiel galiléen et un référentiel galiléen est un référentiel où la première loi de Newton s'applique… ce qui semble être une définition circulaire. Pour éviter ce problème, on peut réécrire le principe d'inertie comme suit :

« Il existe une famille de référentiels, appelés galiléens ou inertiels, tels que, par rapport à l'un de ces référentiels, tout point matériel isolé (qui n'est soumis à aucune action extérieure) est soit au repos, soit animé d'un mouvement rectiligne et uniforme. »

La détermination d'un bon référentiel galiléen est en réalité expérimentale et comme souvent en Physique, seule la cohérence entre la théorie (ici la première loi de Newton) et la mesure (mouvement rectiligne uniforme) valide le choix a posteriori.

Troisième loi de Newton ou principe des actions réciproques

« Tout corps A exerçant une force sur un corps B subit une force d'intensité égale, de même direction mais de sens opposé, exercée par le corps B ».

A et B étant deux corps en interaction, la force (exercée par A sur B) et la force (exercée par B sur A) qui décrivent l'interaction sont directement opposées :

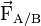
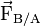
Dans le cas de la mécanique du point, la troisième loi précise également :

 : la force d'interaction est portée par la droite reliant les positions des particules.

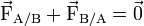
Ces forces ont la même droite d'action, des sens opposés et la même norme. Ces deux forces sont toujours directement opposées, qu'A et B soient immobiles ou en mouvement.

Cette loi est parfois appelée loi d'action - réaction, une formulation au mieux imprécise, au pire entraînant de nombreuses confusions. En particulier, cette ancienne formulation véhicule l'idée qu'il y a toujours une force qui est la « cause » (l'action), l'autre n'étant qu'une sorte de conséquence (la réaction).

Une autre difficulté rencontrée par les étudiants est l'oubli que ces deux forces et s'exercent sur deux corps différents. Elles ne peuvent donc pas « s'annuler mutuellement ». L'effet d'annulation n'intervient que lorsqu'on considère un système constitué de différents corps et que l'on s'intéresse à la résultante des forces : dans ce cas, les forces intérieures s'annulent en effet et seule la somme des forces extérieures est à prendre en compte (ce qui est heureux pour étudier le mouvement d'un solide constitué de plus de 10²³ éléments).

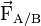
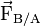
La loi des actions réciproques a l'inconvénient de supposer l'application des forces comme instantanée (ce qui est abandonné en relativité restreinte). Dans le cas des forces à distance, il convient dans certains cas d'effectuer des transformations pour tenir compte du retard de propagation.

Cette correction ne relève pas de la relativité. Comme les forces électromagnétiques s'appliquent à distance, on avait mis en évidence que ces forces se propagent à la vitesse de la lumière et non à vitesse infinie et inclus cette nuance dans les équations avant la révolution de la relativité restreinte.