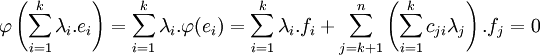Matrice génératrice - Définition

Définitions

Une notion naturelle apparait et donne lieu à la définition suivante :

• La matrice génératrice G d'un code linéaire est la matrice de l'application linéaire d'encodage φ dans les bases canoniques.

L'égalité suivante est naturellement vérifiée d'après les propriétés des matrices :

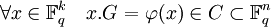
On remarque que la dimension de la matrice génératrice est k x n car E est de dimension k et F de dimension n.

• Deux matrices génératrices G et G' sont dit équivalentes si et seulement s'il existe une matrice carrée P d'un automorphisme de E tel que : G' = G.P.

Les codes de longueur k et de dimension n sur un même corps fini possèdent exactement les mêmes propriétés si leurs matrices génératrices sont équivalentes. En particulier, ils possèdent la même distance minimale. En effet, l'image de φ, c’est-à-dire le code reste inchangé par toute permutation préalable sur l'ensemble E, en particulier par un automorphisme. Il n'en est pas de même pour F, un automorphisme peut associer à deux vecteurs à une distance de Hamming de δ, deux vecteurs à une distance de un, ce qui détruirait toutes les propriétés du code.

Propriétés

Code systématique

Il existe une forme de la matrice génératrice particulièrement simple, ce qui donne lieu à la définition suivante :

• Un code linéaire dont la matrice génératrice possède pour k premières colonnes une matrice identité est dit code systématique.

La matrice prend alors la forme suivante :

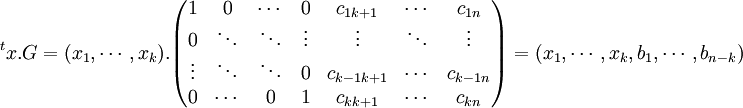
Cette forme est particulièrement intéressante, le calcul du mot de code consiste à la détermination des n - k dernières coordonnées, car les k premières correspondent à celles du message initial. De plus, sous réserve d'absence d'altération, le décodage est lui aussi rapide, il consiste à ne considérer uniquement les n premières coordonnées du mot du code. On remarque au passage que le nombre de lignes de la matrice génératrice est égale à l'ordre du vecteur à coder (ici noté k), sans quoi le produit matriciel n'a pas de sens.

• Les n - k dernières colonnes (c_ij) de la matrice génératrice sont appelées contrôles de redondance.
• Les n - k dernières coordonnées (b_j) d'un code systématique sont dit bits de contrôle ou parfois somme de contrôle.

Ces coordonnées correspondent exactement à la redondance, leur objectif est la détection ou la correction d'erreurs éventuelles. Dans le cas binaire, elles correspondent à la parité de sommes de lettres du message d'origine, on parle alors souvent de bits de parité.

Les codes linéaires peuvent tous se mettre sous cette forme :

• Tout code linéaire est équivalent à un code systématique.

Ce qui signifie que, quitte à modifier la base de E, il est possible d'exprimer la matrice génératrice du code grâce à une matrice systématique.

Remarquons tout d'abord qu'il est peut être nécessaire de modifier l'ordre de la base canonique de F. En effet, si par exemple, le code est inclus dans l'espace vectoriel engendré par les n - 1 derniers vecteurs de la base canonique, alors il est vain de chercher une forme systématique sans modifier l'ordre de la base. En revanche, une permutation des vecteurs ne modifie pas la distance de Hamming.

Montrons tout d'abord le lemme suivant:

• La plus grande famille de vecteurs de la base canonique engendrant un sous-espace vectoriel d'intersection réduite au vecteur nul avec le code est de cardinal n - k.

C'est une conséquence directe du théorème de la base incomplète. En effet, considérons une base du code, elle forme une famille libre. Le théorème de la base incomplète indique qu'il est possible de compléter cette base par des éléments d'une famille génératrice quelconque, par exemple la base canonique de F. Les vecteurs complétant la famille sont au nombre de n - k car le code est de dimension k et F de dimension n. Ces vecteurs forment une famille répondant aux hypothèses de la proposition. Toute famille de cardinal supérieur possède une codimension supérieure à la dimension du code et donc l'intersection de l'espace généré par une telle famille et le code est non réduit au vecteur nul.

Démontrons alors la proposition:

• Tout code linéaire est équivalent à un code systématique.

Soit (f_j) où j est un entier compris entre 1 et n la base canonique de F. Quitte à la réordonner, supposons que les n - k derniers vecteurs engendrent un sous-espace d'intersection réduite au vecteur nul avec le code.

L'objectif est de trouver une base de E (e_i) où i est un entier compris entre 1 et k tel que :

Soit V_i de F le sous-espace vectoriel engendré par les vecteurs f_j où j est élément de l'union des ensembles {i} et [k + 1, n], où i est choisi élément de [1, k]. V_i contient une intersection non vide avec le code φ(E). En effet, la dimension du code est strictement supérieure à la codimension de V_i. Un élément non nul de cette intersection possède une coordonnée sur f_i non nulle car les n - k derniers vecteurs de la base engendre un sous-espace vectoriel d'intersection réduite au vecteur nul avec le code. Choisissons l'élément de l'intersection ayant une coordonnée égal à 1 sur le vecteur f_i et notons e_i son antécédent par φ. Les k égalités décrites en (ii) sont vérifiées.

Il ne reste plus qu'à montrer que la famille (e_i) est libre. Considérons une relation de dépendance linéaire de cette famille  :

L'image par φ de cette relation de dépendance linéaire est encore nulle donc :

Or la famille (f_j) est une base, donc la relation de dépendance linéaire sur cette base est triviale, ce qui démontre la nullité des coefficients λ_i. La famille (e_i) est donc libre, c'est une base car son cardinal est celui de la dimension de E, ce qui termine la démonstration.