Mécanisme de Englert-Brout-Higgs-Guralnik-Hagen-Kibble - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Exemple: la brisure électrofaible

Introduction

En physique des particules le mécanisme de Englert–Brout–Higgs–Guralnik–Hagen–Kibble, souvent abrégé (au détriment de certains auteurs) mécanisme de Brout-Englert-Higgs, voire mécanisme de Higgs, introduit indépendamment par François Englert et Robert Brout, par Peter Higgs, et par Gerald Guralnik, Carl Richard Hagen et Tom Kibble en 1964, décrit un processus par lequel une symétrie locale de la théorie peut être brisée spontanément en rendant massifs ses bosons de jauge lorsqu'un champ scalaire, appelé boson de Higgs acquiert une valeur moyenne non nulle dans le vide.

Kibble, Guralnik, Hagen, Englert, et Brout lors de la remise du Prix Sakurai 2010.

Exemple: la brisure électrofaible

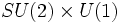
Dans le cadre du Modèle standard c'est le mécanisme de Higgs qui brise l'interaction électrofaible basée sur le groupe de jauge $SU(2)\times U(1)\,$ en donnant une masse non nulle à plusieurs de ces bosons de jauge et plus précisément les bosons W et Z alors que le photon lui reste de masse nulle. En conséquence l'interaction faible qui est transportée par les bosons W et Z (et dont le groupe de jauge est $SU(2)\,$ ) est à courte portée (de l'ordre de 10^-18 m) alors que l'interaction électromagnétique qui est transportée par le photon (et dont le groupe de jauge est $U(1)\,$ )est dite de portée infinie ce qui est un synonyme pour dire qu'elle est visible macroscopiquement. De façon indirecte le mécanisme de Higgs est également la source de la masse non nulle de tous les fermions qui composent la matière.

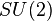
Motivations

Le modèle standard repose en grande partie sur les concepts de symétrie et d'invariance, notamment l'invariance de jauge qui génère les interactions. Cette invariance concerne notamment le Lagrangien du modèle, et interdit d'introduire des termes de masse pour les bosons de jauges, vecteurs de l'interaction. Or on sait aujourd'hui que certains de ces bosons (les W et le Z de l'interaction faible ) ont une masse. Le défi consiste donc à générer ces termes de masse dans le Lagrangien en évitant de remettre en cause tout ce bel édifice théorique.

Principes

L'idée consiste alors à introduire un champ scalaire $φ$ particulier, caractérisé par son potentiel, choisi de sorte à avoir un état du vide non nul.

Ce champ scalaire est un doublet de $S U (2)$ , et le potentiel le plus général qui soit invariant et renormalisable qui lui correspond est

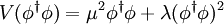
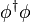
construit à l'aide de la quantité invariante $\phi^\dagger \phi$ , avec $λ$ nécessairement positif puisqu'on souhaite avoir un état d'énergie la plus basse.

Afin d'avoir la brisure de symétrie recherchée, il faut considérer $μ 2 < 0$ , ainsi l'état du vide n'est plus invariant par rotation dans $S U (2)$ .

À basse énergie, il est commode de développer les calculs autour de ces minimas d'énergie. C'est ce développement qui est à l'origine de la brisure de symétrie, en ne considérant que certains termes d'ordre les plus bas.

Les termes de masses apparaissent alors naturellement.

Ici, les deux lagrangiens, avant et après brisure, sont bien équivalents, et la physique reste la même. Si l'on pouvait résoudre exactement les équations dynamiques avant brisure, on aurait une dynamique avec des bosons sans masse, mais dont l'interaction avec le champ de Higgs conduit à un comportement équivalent à celui de bosons massifs. Le développement autour du vide permet simplement de faire apparaître explicitement des termes qui ont les bonnes propriétés pour être interprétés comme des masses.