Mercredi 18 Juin 2025
Rechercher 🔍

Méthode chakravala - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Objectif - Apports de Brahmagupta - Histoire - Démonstrations associées à l'apport de Bhaskara II - Apport de Bhaskara II - Fraction continue

Apport de Bhaskara II

Principe de la méthode

Une difficulté de la méthode de Brahmagupta réside dans le fait qu'il n'est pas toujours simple de trouver un nombre α de A de norme dans l'ensemble des nombres en valeur absolue égales à 1, 2 ou 4. L'apport de Bhaskara II décrit dans le Siddhanta Siroman consiste à enrichir la méthode d'un algorithme qui finit infailliblement par fournir une quasi-solution de cette nature.

Bhaskara II construit une suite récurrente (αn) d'éléments de A de la manière suivante :

Le premier élément α1 de la suite est de la forme a1 + √n. Il est choisi de telle manière à ce que la norme de α1, égale à a12 - n, soit la plus petite possible en valeur absolue.

Supposons la suite définie à l'ordre j. On note αj = aj + bj.√n. On construit un élément βj = mj + √n. Le nombre entier mj est tel que aj + mj.bj soit dans un multiple de la norme de αj et mj minimise la valeur absolue de la norme de βj. L'élément αj + 1 est défini de la manière suivante :

\alpha_{j+1} = a_{j+1} + b_{j+1} \sqrt n = \frac 1{|\mathcal N(\alpha_j)|} \alpha_j \beta_j=\frac 1{|\mathcal N(\alpha_j)|} \left( a_jm_j + nb_j + \sqrt n(a_j + m_jb_j)\right)\;

Exemples

Défi de Fermat

Choisissons encore d égal 61. La valeur de a 1 est égale à 8 pour minimiser la norme de α1, en effet :

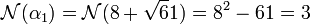
\mathcal N(\alpha_1) = \mathcal N(8 + \sqrt 61) = 8^2 - 61 = 3\;

Pour déterminer la valeur de α2 il est nécessaire de calculer m 1. On dispose de l'égalité suivante :

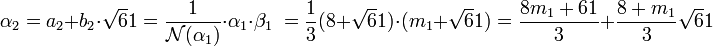
\alpha_2 = a_2 + b_2\cdot \sqrt 61 = \frac 1{\mathcal N(\alpha_1)}\cdot \alpha_1\cdot \beta_1\; =\frac 13(8 + \sqrt 61)\cdot (m_1 + \sqrt 61) = \frac {8m_1 + 61}{3} + \frac{8 + m_1}{3} \sqrt 61 \;

Comme α2 est un élément de A, 8 + m 1 est un multiple de 3, ou encore m 1 est de la forme 3.k + 1. Pour minimiser la norme de β1, il faut choisir k égal à 2. On en déduit que m 1 est égal à 7, ce qui donne :

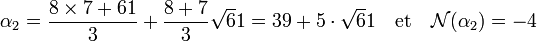
\alpha_2 = \frac {8\times 7 + 61}{3} + \frac{8 + 7}{3} \sqrt 61 = 39 + 5\cdot \sqrt 61 \quad \text{et}\quad \mathcal N(\alpha_2) = -4\;

La suite de la méthode est celle de Brahmagupta. La méthode chakravala permet maintenant de résoudre sans tâtonnement et avec un minimum de calcul le défi de Fermat.

Exemple de Narayana

Ce deuxième exemple est aussi extrait du Siddhanta Siroman de Bhaskara II, annoté par Narayana. Si d est égal à 103, la valeur de a 1 est égale à 10 et :

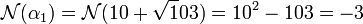
\mathcal N(\alpha_1) = \mathcal N(10 + \sqrt 103) = 10^2 - 103 = -3\;

Le calcul de α2 donne :

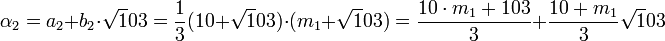
\alpha_2 = a_2 + b_2\cdot \sqrt 103 = \frac 13(10 + \sqrt 103)\cdot (m_1 + \sqrt 103)=\frac {10\cdot m_1 + 103}{3} + \frac{10 + m_1}{3} \sqrt 103\;

Cette fois ci, m 1 est de la forme 3.k - 1. Pour minimiser la norme de β1, il faut choisir m 1 égal à 11. On obtient :

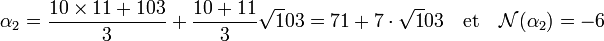
\alpha_2 = \frac {10\times 11 + 103}{3} + \frac{10 + 11}{3} \sqrt 103 = 71 + 7\cdot \sqrt 103 \quad \text{et}\quad \mathcal N(\alpha_2) = -6\;

Le calcul de α3 donne :

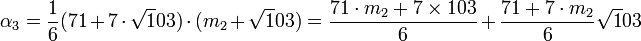
\alpha_3 = \frac 16(71 + 7\cdot \sqrt 103)\cdot (m_2 + \sqrt 103)=\frac {71\cdot m_2 + 7\times 103}{6} + \frac{71 + 7\cdot m_2}{6} \sqrt 103\;

Cette fois ci, m 2 est de la forme 6.k - 5. Pour minimiser la norme de β2, il faut choisir m 2 égal à 7. On obtient :

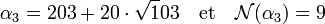
\alpha_3 = 203 + 20\cdot \sqrt 103 \quad \text{et}\quad \mathcal N(\alpha_3) = 9\;

Le calcul de α4 donne :

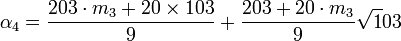
\alpha_4 = \frac {203\cdot m_3 + 20\times 103}{9} + \frac{203 + 20\cdot m_3}{9} \sqrt 103\;

Cette fois ci, m 3 est de la forme 9.k + 2. Pour minimiser la norme de β3, il faut choisir m 3 égal à 11. On obtient :

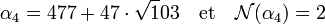
\alpha_4 = 477 + 47\cdot \sqrt 103 \quad \text{et}\quad \mathcal N(\alpha_4) = 2\;

Le calcul de Brahmagupta permet de conclure, la valeur α cherchée est égal à 1/2.α42 :

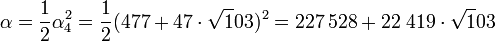
\alpha = \frac 12 \alpha_4^2 =\frac 12 (477 + 47\cdot \sqrt 103)^2 = 227\,528 + 22\;419\cdot \sqrt 103

Fraction continue

La partie récursive de la méthode chakravala est très proche de celle de la fraction continue. Ici, l'objectif est d'approximer la racine de n par une expression optimale de la nature suivante :

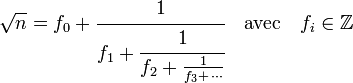
\sqrt n = f_0 + \cfrac{1}{f_1 + \cfrac{1}{f_2 + \frac{1}{f_3+\,\cdots}}}\quad \text{avec}\quad f_i \in \mathbb Z \;

Introduction par l'exemple

Étudions le cas où n est égal à 19.

A l'ordre 0, l'objectif est de trouver la valeur f0 la plus proche possible de √19. On obtient l'égalité :

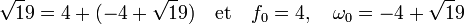
\sqrt 19 = 4 + (-4 + \sqrt 19) \quad\text{et}\quad f_0 = 4,\quad \omega_0 = -4 + \sqrt 19

Ici, ωk désigne le reste de la fraction continue, souvent appelé quotient complet d'indice k.

A l'ordre 1, on cherche une approximation √19 de la forme f0 + 1/f1 la meilleure possible, on obtient :

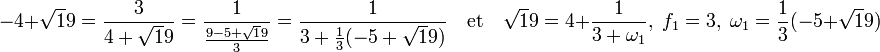
-4 + \sqrt 19 = \frac 3{4 + \sqrt 19} = \frac 1{\frac{9 - 5 + \sqrt 19}3} = \frac 1{3 + \frac13(-5 + \sqrt 19)}\quad\text{et}\quad \sqrt 19 = 4 + \frac 1{3 + \omega_1},\; f_1 = 3,\; \omega_1 = \frac 13(-5 + \sqrt 19)

A l'ordre 2 :

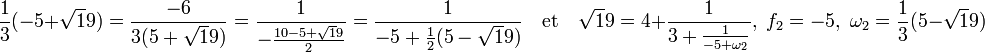
\frac 13(-5 + \sqrt 19) = \frac {-6}{3(5 + \sqrt 19)} = \frac 1{-\frac{10 - 5 + \sqrt 19}2} = \frac 1{-5 + \frac12(5 - \sqrt 19)}\quad\text{et}\quad \sqrt 19 = 4 + \frac 1{3 + \frac 1{-5 + \omega_2}},\; f_2 = -5,\; \omega_2 = \frac 13(5 - \sqrt 19)

A l'ordre 3 :

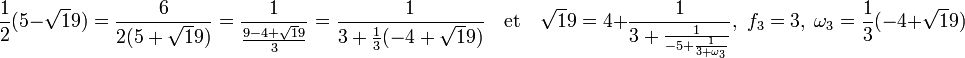
\frac 12(5 - \sqrt 19) = \frac {6}{2(5 + \sqrt 19)} = \frac 1{\frac{9 - 4 + \sqrt 19}3} = \frac 1{3 + \frac13(-4 + \sqrt 19)}\quad\text{et}\quad \sqrt 19 = 4 + \frac 1{3 + \frac 1{-5 + \frac 1{3 +\omega_3}}},\; f_3 = 3,\; \omega_3 = \frac 13(-4 + \sqrt 19)

A l'ordre 4 :

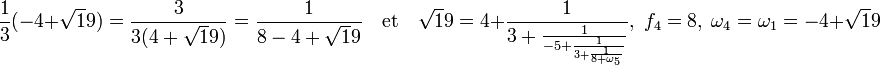
\frac 13(-4 + \sqrt 19) = \frac {3}{3(4 + \sqrt 19)} = \frac 1{8 - 4 + \sqrt 19} \quad\text{et}\quad \sqrt 19 = 4 + \frac 1{3 + \frac 1{-5 + \frac 1{3 +\frac 1{8 +\omega_5}}}},\; f_4 = 8,\; \omega_4 = \omega_1 = -4 + \sqrt 19

Le fait que ω4 soit égal à ω0 montre que la suite (fk) est périodique, ces termes sont : f0, f1, f2, f3, f4, f1, f2, f3, f4, f1, ... . On note généralement une égalité de ce type de la manière suivante :

\sqrt 19 = [4, \overline{3,-5,3,8}]

Déterminons les fractions partielles à l'ordre k θk, habituellement appelées réduite d'indice k.

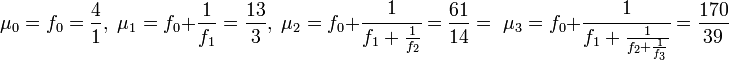
\mu_0 = f_0 = \frac41,\; \mu_1 = f_0 + \frac 1{f_1}= \frac {13}3,\; \mu_2 = f_0 + \cfrac 1{f_1 + \frac 1{f_2}} =\frac {61}{14} = \; \mu_3 = f_0 + \cfrac 1{f_1 + \frac 1{f_2 + \frac 1{f_3}}} =\frac {170}{39}

Le calcul de la suite (αk) de la méthode chakrala donne :

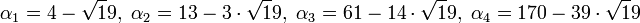
\alpha_1 = 4 - \sqrt 19,\; \alpha_2 = 13 - 3\cdot \sqrt 19,\; \alpha_3 = 61 - 14\cdot\sqrt 19,\; \alpha_4 = 170 - 39\cdot \sqrt 19

On trouve dans les deux cas les mêmes couples (4,1), (13, 2), (61, 14) et (170, 39), ce qui n'est pas l'œuvre du hasard. Dans les deux cas on obtient la solution suivante :

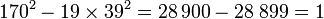
170^2 - 19\times 39^2 = 28\,900 - 28\;899 = 1\;


Remarque : La convention choisie ici pour définir la fraction est que chaque réduite d'indice k doit être aussi proche que possible de la racine. La convention d'une fraction continue est un peu différente. Non seulement chaque réduite d'indice k doit être aussi proche que possible de la racine mais de plus la suite (fk) doit ne prendre que des valeurs positives. La convention des fractions continues peut aussi s'appliquer à la méthode de chakravala, elle revient à imposer à la suite des normes des (βk) d'être strictement négative. Toutes les démonstrations s'appliquent encore avec cette convention. En revanche, la longueur du cycle peut être plus longue, par exemple :

\sqrt 19 = [4, \overline{2,1,3,1,2,8}]

Approche théorique

Soit (fk) et (θk) où k est un entier positif, deux suites dont la première est à valeur dans Z et la deuxième dans A. Les suites sont définies par récurrence. La valeur f0 est égale à la partie entière de √n, où n est un entier strictement supérieur à 1 et sans facteur carré, et θ0 l'élément de A défini par l'égalité :

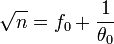
\sqrt n = f_0 + \frac 1{\theta_0}

La valeur 1 / fk+1 est la meilleure approximation de θk et θk+1 est l'élément de A vérifiant l'égalité :

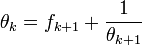
\theta_k = f_{k+1} + \frac 1{\theta_{k+1}}

Cette définition diffère légèrement de la traditionnelle fraction continue car fk n'est pas nécessairement choisi positif. On remarque de fk+1 et le plus grand entier plus petit que 1/θk. Le fait que √n soit irrationnel montre que θk est toujours irrationnel, les suites (fk) et (θk) ne prennent jamais la valeur 0 et sont ainsi bien définies.

Soit (c k) et (d k) les deux suites de Z telles que pour tout k, c k et c d soient premiers entre eux et la fraction c k / d k soit égale à la fraction réduite d'indice k.

  • Pour tout nombre entier k, si (αk) et (βk) désignent les suites de la méthode chakravala définies précédemment, les égalités suivantes sont vérifiées :
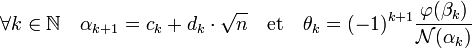
\forall k \in \mathbb N \quad \alpha_{k+1} = c_k + d_k\cdot \sqrt n \quad \text{et}\quad \theta_k = (-1)^{k+1}\frac {\varphi(\beta_k)}{\mathcal N(\alpha_k)}\;

Ainsi, la méthode chakravala permet de démontrer le caractère périodique et la propriété de palindrome d'une fraction continue. Si l'algorithme récursif impose à la suite (βk) d'être aussi de norme systématiquement négative, alors les démonstrations de l'article restent valables et les fractions continues associées correspondent à la définition usuelle, c'est-à-dire que les suites (fk) et (θk) sont à valeurs strictement positives.

Un lemme est utile pour établir la proposition de ce paragraphe :

  • La condition de congruence sur βk est équivalente au fait que pour tout k strictement positif mk-1 + mk soit un multiple de la norme de αk.

En d'autres termes, l'équivalence suivante est vérifiée :

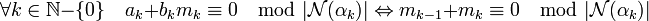
\forall k \in \mathbb N - \{0\} \quad a_k + b_km_k \equiv 0 \mod |\mathcal N(\alpha_k)| \Leftrightarrow m_{k-1} + m_k \equiv 0 \mod |\mathcal N(\alpha_k)|

En effet, a k et b k sont premiers entre eux, cette propriétés est démontrée dans le paragraphe sur les lemmes. L'égalité suivante montre que b k et la norme de αk sont aussi premiers entre eux :

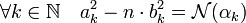
\forall k \in \mathbb N\quad a_k^2 - n\cdot b_k^2 = \mathcal N (\alpha_k)

L'élément b k est en conséquence inversible dans l'anneau Z / N(αk)Z. Soit g k son inverse. La condition de congruence est équivalente à la suivante :

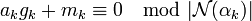
a_kg_k + m_k \equiv 0 \mod |\mathcal N(\alpha_k)|

La proposition à démontrer est équivalente à l'une des deux formes suivantes :

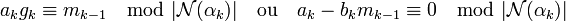
a_kg_k \equiv m_{k-1} \mod |\mathcal N(\alpha_k)| \quad \text{ou}\quad a_k - b_km_{k-1} \equiv 0 \mod |\mathcal N(\alpha_k)|

On reconnaît là la deuxième coordonnée de l'élément αk φ(βk-1), en effet :

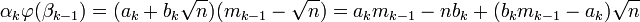
\alpha_k\varphi(\beta_{k-1}) = (a_k + b_k\sqrt n)(m_{k-1} - \sqrt n) = a_k m_{k-1} - nb_k + (b_km_{k-1} - a_k)\sqrt n \;

Il suffit donc de démontrer que αk φ(βk-1) est un multiple de la norme de αk pour établir le lemme, ou encore, comme la norme de αk est égale au produit αk. φ(αk), il suffit de montrer que φ(βk-1) est un multiple de φ(αk). Une manière plus simple prouver le lemme est de montrer que βk-1 est un multiple de αk. Les égalités suivantes, issues de la définition de αk permettent de conclure :

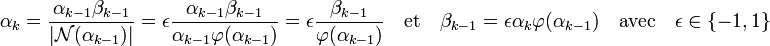
\alpha_k = \frac {\alpha_{k-1}\beta_{k-1}}{|\mathcal N(\alpha_{k-1})|} = \epsilon\frac {\alpha_{k-1}\beta_{k-1}}{\alpha_{k-1}\varphi (\alpha_{k-1})} = \epsilon \frac {\beta_{k-1}}{\varphi(\alpha_{k-1})} \quad \text{et}\quad \beta_{k-1} = \epsilon \alpha_k\varphi(\alpha_{k-1})\quad \text{avec}\quad \epsilon \in \{-1,1\}
  • Pour tout nombre entier k, θk = (-1)k+1 φ(βk) / N(αk) :

Montrons ce résultat par récurrence, sur k.

Si k est égal à zéro :

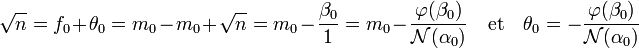
\sqrt n = f_0 + \theta_0 = m_0 - m_0 + \sqrt n = m_0 - \frac {\beta_0}{1} = m_0 - \frac {\varphi(\beta_0)}{\mathcal N (\alpha_0)}\quad \text{et}\quad \theta_0 = - \frac {\varphi(\beta_0)}{\mathcal N (\alpha_0)} \;

Supposons le résultat établi à l'ordre k - 1, montrons qu'il est vrai à l'ordre k.

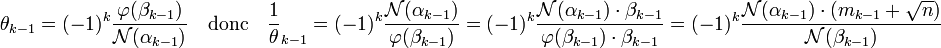
\theta_{k-1} = (-1)^k \frac {\varphi(\beta_{k-1})}{\mathcal N (\alpha_{k-1})}\quad\text{donc}\quad \frac 1\theta_{k-1} = (-1)^k \frac {\mathcal N (\alpha_{k-1})}{\varphi(\beta_{k-1})}= (-1)^k \frac {\mathcal N (\alpha_{k-1})\cdot \beta_{k-1}}{\varphi(\beta_{k-1})\cdot \beta_{k-1}} = (-1)^k \frac {\mathcal N (\alpha_{k-1})\cdot(m_{k-1} + \sqrt n)}{\mathcal N (\beta_{k-1})}\;

Une égalité établie dans le lemme montre que βk-1 est égal au produit de +/-1, αk et de φ(αk-1), on en déduit :

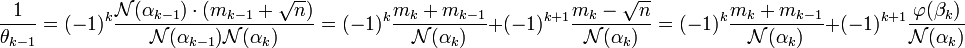
\frac 1{\theta_{k-1}}= (-1)^k \frac {\mathcal N (\alpha_{k-1})\cdot(m_{k-1} + \sqrt n)}{\mathcal N (\alpha_{k-1})\mathcal N (\alpha_k)} = (-1)^k \frac {m_k + m_{k-1}}{\mathcal N (\alpha_k)} + (-1)^{k+1} \frac {m_k - \sqrt n}{\mathcal N (\alpha_k)}= (-1)^k \frac {m_k + m_{k-1}}{\mathcal N (\alpha_k)} + (-1)^{k+1}\frac {\varphi(\beta_k)}{\mathcal N (\alpha_k)} \;

Le lemme montre que mk est choisi de telle manière à ce que (-1)k(mk + mk+1)/ N(αk) soit un entier et (-1)k+1.βk-1 / N(αk) de valeur absolue la plus petite possible.

  • Pour tout nombre entier k, αk+1 est égal à ck + dk√n :

Pour simplifier les calculs, modifions légèrement la définition de αk. Dans cette démonstration, αk+1 est défini comme le produit : 1/N(αk).αk.βk. Ainsi, si la norme de αk est négative, alors les deux coordonnées de αk+1 sont négatives. On remarque immédiatement que la modification des signes des coordonnées de la suite (αk) ne modifie ni la suite (βk) ni les valeurs absolues des coordonnées de la suite (αk). L'objectif est maintenant de démontrer, avec ces nouvelles conventions que αk = (-1)k(ck + dk√n). On dispose des égalités suivantes :

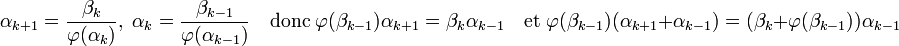
\alpha_{k+1} = \frac {\beta_k}{\varphi(\alpha_k)},\; \alpha_k = \frac {\beta_{k-1}}{\varphi(\alpha_{k-1})} \quad\text{donc}\; \varphi(\beta_{k-1})\alpha_{k+1} = \beta_k\alpha_{k-1}\quad \text{et}\; \varphi(\beta_{k-1})( \alpha_{k+1} + \alpha_{k-1}) = (\beta_k + \varphi(\beta_{k-1}))\alpha_{k-1}

En remplaçant αk-1 par une valeur équivalente et βk + φ(βk+1) par ses coordonnées, on obtient :

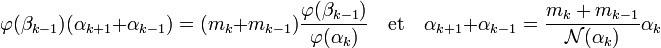
\varphi(\beta_{k-1})( \alpha_{k+1} + \alpha_{k-1}) =(m_k + m_{k-1})\frac {\varphi (\beta_{k-1})}{\varphi(\alpha_k)} \quad\text{et}\quad \alpha_{k+1} + \alpha_{k-1} = \frac {m_k + m_{k-1}}{\mathcal N(\alpha_k)}\alpha_k

On reconnait le terme f k de la fraction continue calculée pour la démonstration précédente. Si α'k est défini comme égal à -(1)kαk :

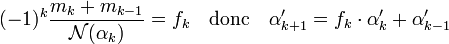
(-1)^k\frac {m_k + m_{k-1}}{\mathcal N(\alpha_k)} = f_k \quad \text{donc}\quad \alpha'_{k+1} = f_k \cdot\alpha'_k + \alpha'_{k-1}\;

Notons αk = ck+1 + dk+1√n et α0 = 1. Les suites (α'k) et (αk) sont égales pour k égale à 0 ou à 1 et elles vérifient toutes les deux la relation de récurrence

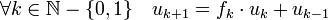
\forall k \in \mathbb N -\{0,1\} \quad u_{k+1} = f_k\cdot u_k + u_{k-1}\;

Les deux suites (α'k) et (αk) sont donc toujours égales. La suite (αk) est égale à la suite (α'k) au signe près. Or elles ont toutes les deux des coefficients toujours strictement positifs, la suite (αk) est donc égale à la suite (αk), ce qui démontre la proposition.

 

Méthode de calcul

L'approche par les fractions continues offre un enrichissement de la méthode algorithmique précédente pour l'équation de Pell-Fermat ou la détermination de la fraction continue. Illustrons ces méthodes à l'aide de l'exemple n = 313 et montrons comment Brouncker pouvait effectivement résoudre ce défi en une heure ou deux. Par définition α0 est égal à 1 et α1 = β0 = 18 + √313 car 182 est la meilleure approximation de 313 dans les carrés parfaits, la norme de α1 est égal à 11. On en déduit la valeur de f 0 = 18.

Pour le calcul de m1, il suffit de remarquer que m1 + m0 est un multiple de 11 et que m12 est la meilleure approximation possible de 313, on trouve m1 = 15. On calcule ensuite celle β1 égale à 152 - 313 = -88. Pour le calcul de la norme de α2 il suffit de remarquer qu'elle est le quotient de celle de β1 par celle de α1, on trouve -8. Pour le calcul de f 1 on utilise la formule du paragraphe précédent, on trouve f 1 = - 1/11 (18 + 15) = -3.

Pour le calcul des valeurs ak et bk, on utilise la formule de récurrence. On construit ainsi le tableau suivant :

Indice mk N(βk) = mk2 - 313 N(αk) = N(βk-1)/N(αk-1) fk = (-1)k(mk + mk-1)/N(αk) ak = fk-1.ak-1 + ak-2 bk = fk-1.bk-1 + bk-2
0 18 11 1 m0 = 18 1 0
1 15 -88 11 -3 18 1
2 17 -24 -8 -4 -53 -3
3 19 48 3 -12 230 13
4 13 -144 16 2 -2 813 -159
5 14 -117 -9 3 -5 396 -305
6 12 -169 13 2 -19 001 -1 074
7 14 -117 -13 2 -43 398 -2 453


Cette approche permet d'éviter les grands nombres, sauf pour les colonnes a k et b k. On remarque que la norme de α7 est l'opposée de cette de α8, ce qui montre que ces deux nombres sont à un facteur inversible près l'image par la fonction φ l'un de l'autre. La suite des normes est donc 1, 11, -8, 3, 16, -9, 13, -13, 9, -16, -3, 8, -11, -1. On en déduit que 1/13.α7.α8 est un élément de norme -1 :

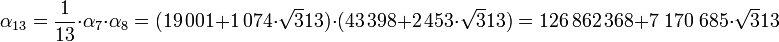
\alpha_{13}=\frac 1{13}\cdot \alpha_7\cdot \alpha_8 = (19\,001 + 1\,074\cdot \sqrt 313)\cdot(43\,398 + 2\,453\cdot\sqrt 313)= 126\,862\,368 + 7\;170\;685\cdot\sqrt 313

Il faut encore mettre ce nombre α13 au carré pour obtenir la solution recherchée :

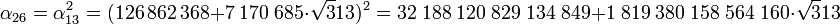
\alpha_{26} =\alpha_{13}^2 = (126\,862\,368 + 7\;170\;685\cdot\sqrt 313)^2 = 32\;188\;120\;829\;134\;849 + 1\;819\;380\;158\;564\;160\cdot\sqrt 313

La méthode chakravala permet ainsi de résoudre à la main ce type de calcul, même si la solution s'exprime de manière un peu fastidieuse. La même démarche, sans le calcul des colonnes a k et b k, inutile pour cet objectif, permet de déterminer la fraction continue √313. Rechercher la solution telle que la suite (f k) ne comporte que des valeurs positives suppose de restreindre le choix aux m k inférieurs ou égaux à 17. On trouve : 17, 1, 2, 4, 11, 1, 1, 3, 2 qui termine cette branche du palindrome. On en déduit que les termes suivants sont : 2, 3, 1, 1, 11, 4, 2, 1. Il est relativement simple de montrer que le terme d'après est nécessairement 34, le double du premier terme. Ce qui donne :

\sqrt 313 = [17, \overline{1,2,4,11,1,1,3,2,2,3,1,1,11,4,2,1,34}]
Démonstrations associées à l'apport de Bhaskara II
- Introduction - Objectif - Apports de Brahmagupta - Histoire - Démonstrations associées à l'apport de Bhaskara II - Apport de Bhaskara II - Fraction continue
miniature
🌍 Découverte: cette règle universelle régit toute vie sur terre
miniature
⏳ L'Univers pourrait disparaître plus tôt que prévu: ce que révèle cette étude
miniature
🌍 Les dernières mesures révèlent un niveau de CO₂ jamais vu depuis 4 millions d'années
miniature
🛡️ Le paradoxe des gangs de rue
miniature
💰 Quelle quantité d'or existe-t-il vraiment sur Terre ?
miniature
🦟 Pourquoi les moustiques sont plus nombreux et piquent davantage en été ?
miniature
1
⚫ Ces trous noirs interagissent avec la lumière fossile du Big Bang
miniature
🦕 Et si les dinosaures détenaient le secret pour vaincre le cancer ?
miniature
😎 Comment font les lunettes de soleil pour filtrer les UV ?
miniature
🚶‍♂️‍➡️ La marche des babouins éclaire l'évolution de la bipédie humaine
miniature
🔭 James Webb capture cette image directe d'une étrange planète à 60 années-lumière
miniature
🦋 Pourquoi et comment les chenilles deviennent-elles des papillons ?
miniature
1
🔭 Voici la plus grande carte de l'Univers. Ses révélations sont surprenantes !
miniature
😴 Penser que l'on est éveillé alors que l'on dort, normal ?
miniature
🌊 Ce cratère raconte l'histoire de l'eau sur Mars
miniature
🐝 Comment les fleurs attirent-elles les insectes pollinisateurs ?
miniature
💥 La collision entre notre Voie lactée et la galaxie d'Andromède remise en question
miniature
🎶 Pourquoi les oiseaux chantent-ils autant et si fort au printemps ?
miniature
💡 Générer de la lumière à partir du vide, c'est possible
miniature
Découverte d'un deuxième système d'apprentissage dans le cerveau
miniature
☀️ Comment se produit un coup de chaleur et comment s'en protéger ?
miniature
⚽ Comment fonctionne la physique d'un tir puissant au foot ?
miniature
🧠 Un algorithme révèle comment notre cerveau se motive
miniature
🔭 Une si grande planète orbite une si petite étoile, comment est-ce possible ?
miniature
1
🐋 Les baleines développent de nouvelles méthodes pour communiquer avec nous
miniature
🥚 Le noyau de Mars sent l'œuf pourri
miniature
🧠 On sait enfin pourquoi le sémaglutide fait maigrir
miniature
🌱 La vie pourrait renaître sur Europe après la mort de la Terre
miniature
🌿 Confirmation scientifique: ce remède ancestral fait naturellement maigrir, et pas qu'un peu !
miniature
💥 Des astronomes identifient les plus puissantes explosions depuis le Big Bang
miniature
🦕 Ce crâne de stégosaure, le plus complet jamais découvert, réécrit l'histoire
miniature
🛏️ Les punaises de lit, ces compagnons indésirables depuis la préhistoire
miniature
🕸️ Connaissez-vous la toile cosmique, l'architecte de l'Univers ?
miniature
🌋 L'éruption de l'Etna vue depuis l'espace
miniature
🐋 Il y a 20 000 ans, l'Homme fabriquait des outils avec des os de baleines
miniature
🟠 Quel est le rôle de ce labyrinthe sur Mars ?
miniature
🎯 Cette stratégie innovante contre le cancer du sein offre une survie de 100%
miniature
1
💥 Le pulsar à trou noir: un objet qui intrigue les astrophysiciens
miniature
🐒 Première: ces singes kidnappent les bébés d'une autre espèce
miniature
🌍 Découverte d'une super-Terre à l'habitabilité intermittente
miniature
🧠 Ces cellules pourraient jouer un rôle bien plus important que les neurones dans la mémoire
miniature
🛰️ Une carte photographique de la Terre toutes les 35 minutes
miniature
Pourquoi l'oxygène est-il si indispensable à autant d'êtres vivants ?
miniature
🐱 Pourquoi certains chats miaulent et ronronnent plus que d'autres ?
miniature
Découverte: un antidouleur sans effets secondaires
miniature
1
🤔 Ces expériences remettent en question un concept fondamental de la thermodynamique
miniature
Le cannabis réduit de moitié la fonction des vaisseaux sanguins
miniature
Les différences hommes-femmes ne sont pas que génétiques
miniature
🦴 Des paresseux géants de plusieurs tonnes parcouraient autrefois l'Amérique
miniature
James Webb découvre une nouvelle population de trous noirs supermassifs
Page générée en 0.173 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise