Méthode chakravala - Définition
La liste des auteurs de cet article est disponible ici.
Démonstrations associées à l'apport de Bhaskara II
Lemmes
Deux lemmes démontrent l'existence de la suite utilisée par Bhaskara II. Avec les notations des paragraphes précédents et si kj désigne la valeur absolue de la norme de αj, on utilise les éléments suivants :
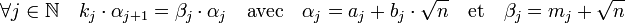
On a choisi mj de telle manière à ce que :
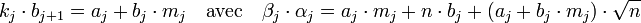
Les deux exemples précédents illustrent le fait que αj.βj est bien un multiple de kj. Cette propriété est l'objet des deux lemmes suivants :
-
- Avec les notations précédentes, si aj + bj.mj est choisi multiple de kj et si aj , bj sont premiers entre eux alors , αj.βj est un multiple de kj.
-
- Sous réserve des hypothèses du lemme précédent et si la norme de βj est choisie minimale en valeur absolue, aj+1, bj+1 sont premiers entre eux.
Une fois ces lemmes démontrés, on remarque qu'il est toujours possible de trouver une valeur convenable pour m j. En effet, comme a j et b j sont premiers entre eux, l'identité de bézout montre qu'il existe un entier c j tel que c j.b j - 1 soit un multiple de k j. On en déduit que si x est un entier, x.k j + c j.b j.a j est un multiple de k j, il est alors toujours possible de choisir x de telle manière à ce que la valeur absolue de la norme de β j soit minimale. Trouver c j revient à résoudre l'identité de Bézout, ce que les indiens savent déjà faire avec l'algorithme d'Euclide.
Les lemmes montrent que si m j est choisi selon la méthode du paragraphe précédent, αj.βj est un multiple de k j, αj+1 est un élément de A et a j+1 et b j+1 sont premiers entre eux deux, ce qui permet de réitérer la démarche.
-
- La valeur αj.βj est un élément de A multiple de k j :
Utilisons les notations suivantes :
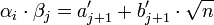
Les éléments a' j+1 et b' j+1 sont des éléments de Z. À ce titre ils peuvent être vu comme des éléments de l'anneau A. Dire que b' j+1 est divisible par k j revient à dire que b' j+1 est divisible par αj.φ(αj), en effet :
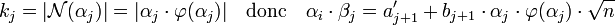
On en déduit l'existence d'un nombre δj de A tel que : αj.δj = a' j+1. Si e j et f j sont deux éléments de Z tel que :
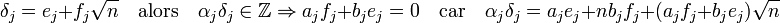
La dernière égalité exprime le fait que les couples (e j, f j) et (a j, -b j) sont proportionnels. Comme a j et b j sont premiers entre eux, il existe un entier a j+1 tel que :
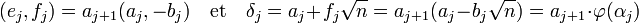
En remplaçant δj par sa valeur dans l'expression αj.δj on obtient :
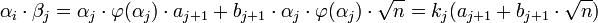
-
- Les valeurs a j+1, b j+1 sont premières entre elles si la valeur absolue de la norme de βj est choisie minimale :
L'égalité suivante est vérifiée :
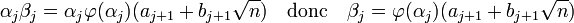
Un entier diviseur commun de a j+1 et b j+1 divise β j ainsi que sa norme. Comme la norme de β j est choisi minimale en valeur absolue, il n'existe aucun diviseur commun à a j+1 et b j+1 autre que 1 et -1.
Caractère cyclique
Une fois montrée que la suite (αj) est bien définie, étudions son comportement. Il est cyclique en un certain sens. Plus précisément, remarquons que la relation R définie par α R β si et seulement si il existe un élément inversible ε de A tel que α = ε.β est une relation d'équivalence. On note cl(α) la classe d'équivalence de α par la relation R :
-
- La suite (cl(αj)) est cyclique.
Cette propriété est la conséquence de trois propositions :
-
- La suite (αj) est définie de manière univoque et la suite (N(αj)) est bornée.
L'égalité N (ε.β) = N(ε).N(β) = N(β) montre que tous les éléments d'une même classe ont même norme. Il est alors possible de parler de la norme d'une classe d'équivalence, ce qui permet l'expression de la proposition suivante :
-
- Il n'existe qu'un nombre fini de classes d'équivalence de norme inférieure à un entier strictement positif.
Enfin :
-
- Soient i et j deux entiers positifs et ε un élément de A inversible. Si αi = ε.αj alors αi+1 = ε.αj+1.
Avec ces trois propriétés, il devient simple de comprendre que la suite (cl(αj) est périodique au bout d'un certain rang. En effet, la suite (N(αj)) est bornée, elle ne prend ces valeurs que dans un nombre fini de classes d'équivalence d'après la proposition deux. Au bout d'un certain rang, la suite a pour image une classe d'équivalence déjà atteinte. La troisième proposition montre que la suite est alors nécessairement périodique.
Ces propriétés ne démontrent que la périodicité à partir d'un certain rang. Le paragraphe suivant montre que ce rang est égal à zéro et la suite est périodique dès l'indice zéro.
-
- La suite (αj) est définie de manière univoque et la suite (N(αj)) est bornée :
Notons r la partie entière de la racine carrée de n. Montrons par récurrence αj est inférieur ou égal à 2.r et que la suite est définie de manière univoque.
Si j est égal à un, On dispose des majorations suivantes :
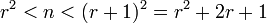
La distance entre les deux carrés parfaits les plus proches encadrant n est égale à 2.r+1, ce qui montre que le carré le plus proche est à une distance inférieure ou égale à r car chaque terme de la majoration est entier. Le fait que le carré le plus proche soit à une distance inférieure ou égal à r et donc à 2.r montre que la norme de α1 est inférieure à 2.r.
Comme n est entier, il ne peut être exactement au milieu de r 2 et (r + 1)2. Il n'existe donc qu'une unique valeur possible pour m 0 et a fortiori pour α1.
Supposons la propriété démontrée à l'ordre j et montrons là à l'ordre j + 1. Soit m' j le plus grand entier inférieur ou égal à r et de la forme aj + m' j.bj soit un multiple de kj. On dispose des majorations suivantes :
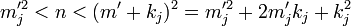
Une fois encore n ne peut se situer exactement au milieu des deux bornes de la majoration, sinon √n serait une fraction, ce qui est contraire à l'hypothèse indiquant que n est sans facteur carré. On en déduit que mj est défini de manière univoque et que n est à une distance de m j2 inférieure ou égale à m' j.kj + 1/2.kj2. Cette majoration et le fait que m j soit inférieur ou égal à r, montrent que la norme de βj est inférieure ou égal à r.kj + 1/2.kj2. Le paragraphe précédent et l'hypothèse de récurrence établissent que :
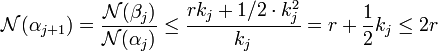
Ce qui montre que la suite est majorée et qu'une valeur du majorant est donnée par 2.r si r désigne la partie entière de la racine carrée de n.
Montrons que la suite les classes des αk est périodique. On remarque que deux éléments d'une même classe possèdent la même norme car la norme d'une unité est égale à 1 en valeur absolue, ce qui permet de donner un sens à la proposition suivante :
-
- Soit C une constante strictement positive. Il n'existe qu'un nombre fini de classes d'équivalences d'éléments de A de norme inférieure à C :
Ce résultat est la conséquence d'un lemme, indiquant qu'il n'existe qu'un nombre fini d'idéaux principaux généré par un élément de norme en valeur absolue inférieure à une constante donnée. Un idéal principal engendré par un élément α de A est l'ensemble des multiples de α dans A. Pour cela, il suffit d'établir la proposition suivante : Soit J un idéal principal engendré par un élément α de norme C un entier strictement positif et B le quotient de A par J.
-
- (1) L'anneau unitaire quotient B est de cardinal fini :
Cette proposition est démontrée dans le paragraphe Idéal premier, idéal maximal de l'article Idéal de l'anneau des entiers d'un corps quadratique.
-
- (3) Il n'existe qu'un nombre fini de classes d'équivalences de norme inférieure à C :
Un idéal ne contient qu'une unique classe d'équivalence de générateurs. En effet, soit α et β deux générateurs d'un tel idéal. L'élément β est généré par α et réciproquement, ce qui montre l'existence d'éléments γ et δ tel que :
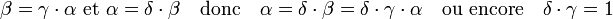
Le caractère fini du nombre d'idéaux et le fait qu'un idéal ne contient qu'une classe d'équivalence permet de conclure la démonstration.
-
- Soient i et j deux entiers positifs et ε un élément de A inversible. Si αi = ε.αj alors αi+1 = ε.αj+1 :
Si αi = ε.αj alors les normes de αi et αj sont égales en valeur absolue car la norme est multiplicative et celle de ε est égale à +/- 1. Le lemme montre que :
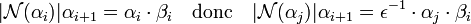
Ce qui montre que βi est un multiple de la norme de αj et comme la norme de βi est choisi minimale, on a bien βi = βj et ceci termine la démonstration.
Structure de la suite
Le fait que la suite soit périodique n'indique a priori pas qu'elle atteint un point de norme égale à un en valeur absolue. Tel est pourtant toujours le cas :
-
- Il existe une valeur j strictement supérieure à zéro et telle que la norme de αj soit égale à 1 en valeur absolue.
La suite (αk) forme une espèce de palindrome, plus précisément si G désigne le groupe des unités :
-
- Selon que la première valeur j strictement positive tel que αj soit de norme égale à un en valeur absolue est paire ou impaire, l'une des deux configurations suivantes se réalise :
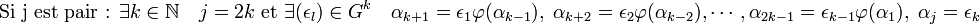
et :
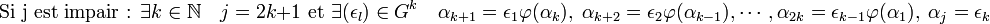
Une conséquence directe est que la suite (αk) contient une solution de l'équation de Pell pour m égal à 1 :
-
- Soit j la plus petite valeur strictement positive telle que la norme de αj soit égale à 1 en valeur absolue, la norme de α2j est strictement positive et égale à 1.
Soit ψ la fonction de A - {0} dans A - {0} qui à αk associe αk+1. Plus précisément à un élément α de A on associe un élément β de forme m + √n avec m entier naturel tel que β.α soit un multiple de la norme de α, de norme minimale et tel que l'égalité N(α).ψ(α) = α.β. Les lemmes et le paragraphe précédent montre que l'application ψ est bien définie et que, si α0 est choisi égal à 1 :
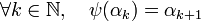
Cette fonction possède une symétrie par rapport à la fonction φ, si G désigne le groupe des unités de A :
-
- La propriété suivante est vérifiée :
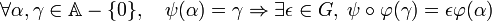
Autrement dit, si α possède pour image par ψ la valeur γ, alors γ possède pour image par ψ la valeur α, à un facteur inversible près.
En effet, si α possède pour image par ψ la valeur γ, il existe un unique élément β de la forme m + √n avec m entier naturel tel que, si ε1 (resp. ε2) est le signe de la norme de α (resp. γ) :

L'élément β est bien de la forme m + √n avec m entier naturel tel que β.γ est un multiple de la norme de γ, car φ(α) est entier. Soit β'un élément vérifiant ces propriétés et de norme inférieure à β, l'égalité γ = α.β'/N(β') montre que β' est de norme supérieure à β. On en déduit que les normes de β et β' sont égales et son caractère minimal est vérifié. L'égalité (1) montre que φ(α), à un élément inversible près est bien l'image de φ(γ) par ψ. La proposition est démontrée.
On en déduit que la fonction ψ est une bijection de A - {0} dans A - {0}.
-
- Il existe une valeur j telle que la norme de αj soit égale à un en valeur absolue :
Remarquons dans un premier temps que l'on peut définir α0 comme égal à 1, car ψ(1) = α1. Soit j la plus grande valeur tel que la suite d'éléments α0, α1, ... , αj-1 ne contienne que des éléments de classes distincts par la relation d'équivalence R. Une telle définition possède un sens car les classes d'équivalences de norme inférieures à 2r sont en nombre fini, la suite des classes d'équivalence se répète donc nécessairement à partir d'un certain rang. La valeur αj est dans la liste α0, α1, ... , αj-1 à un facteur multiplicatif inversible près. Elle ne peut pas être égale à un élément pris dans α1, ... , αj-1 car un tel élément aurait deux antécédents ce que la dernière proposition à montré impossible. On en déduit que la classe de αj est égal à celle de α0. Il suffit de remarquer que la suite des valeurs (ak) et (bk) est strictement croissante pour conclure que la solution trouvée n'est pas triviale.
-
- La suite (αj) forme un palindrome :
L'égalité ψ(1) = α1 montre que ψoφ(α1) est dans classe de φ(1) = 1. On en déduit que cl(αj-1) = cl(φ(α1)). L'égalité ψ(α1) = α2 montre que l' antécédent de la classe de φ (α2) est la classe de φ(α1) ce qui montre que cl(αj-2) = cl(φ(α2)). Une récurrence fondée sur ce principe permet d'établir la proposition.

















































