Méthode chakravala - Définition

Histoire

Mathématiques indiennes

Les mathématiques indiennes s'intéressent très tôt à l'arithmétique. Aryabhata, un mathématicien du VI^e siècle établit les bases de l'arithmétique indienne. Il développe un système de numération montrant qu'il connaissait probablement la notation positionnelle ainsi que l'existence du zéro. Il travaille sur les équations diophantiennes et pour résoudre l'identité de Bézout, met au point un algorithme équivalent à celui d'Euclide qu'il appelle kuṭṭaka (कूटटक) et qui signifie pulvérisateur car il casse les nombres en entiers plus petits. Il travaille aussi sur les fractions continues.

Le mathématicien indien Brahmagupta semble être le premier à analyser en profondeur cette question. Il comprend comment, à partir de deux solutions, il est possible d'en construire une nouvelle. En réitérant, il obtient ainsi un nombre de solutions distinctes aussi élevé que souhaité. Cette méthode est appelée samasa par les mathématiciens indiens. Brahmagupta en déduit trois algorithmes. Le premier lui permet de trouver une solution s'il dispose d'un couple d'entiers (x₀, y₀) dont l'image par l'équation est -1. Il en trouve un deuxième traitant le cas où l'image est 2 en valeur absolue. Il en trouve une troisième donnant le même résultat si l'image est égale à +/- 4. Une première version de la méthode chakravala voit le jour. Elle commence par un tâtonnement jusqu'à trouver un couple ayant pour image 1, 2 ou 4 en valeur absolue, elle continue par l'un des trois algorithmes. Brahmagupta l'utilise en 628 pour résoudre l'équation suivante :

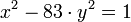
Cette approche est insuffisante pour traiter les cas complexes, il peut être difficile de trouver par tâtonnement un couple donnant une des six valeurs qui permettent de conclure. Au XII^e siècle Bhāskara II innove et propose la forme définitive de la méthode chakravala. Elle correspond à l'adjonction d'un algorithme cyclique, c'est-à-dire donnant une suite périodique de couples contenant nécessairement une solution. L'algorithme cyclique est équivalent à celui des fractions continues. La méthode chakravala termine par les calculs de Brahmagupta si l'une des valeurs -1, +/ 2 et +/- 4 apparaît. Bhāskara II l'utilise pour trouver une solution minimale à l'équation suivante déjà trouvée par Brahmagupta :

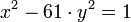
Le couple de solution trouvée est :

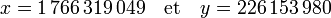
Il est peu probable que Bhāskara II ait démontré le fait que l'algorithme offre toujours une solution, c'est-à-dire pour n'importe quel valeur de n. Deux raisons le laissent penser, tout d'abord la démonstration, longue et technique, demande une sophistication de loin supérieure aux mathématiques du XII^e siècle, ensuite si la preuve avait été trouvée il aurait paru clair que le passage par la méthode de Brahmagupta n'est pas nécessaire, même s'il accélère la convergence de l'algorithme. De nouveaux exemples sont traités plus tard, par les mathématiciens indiens. Au XIV^e siècle un mathématicien du nom de Narayana étudie le cas où n est égal à 103 dans ses commentaires sur le livre Bijaganita' de Bhāskara II.

Europe

Pierre de Fermat lance le 3 janvier 1658 un défi aux mathématiciens européens. Il contient la recherche d'une solution au problème indien avec pour valeur de n 61, déjà traité par Brahmagupta et Bhāskara II. À cette époque l'Europe n'a pas connaissance des résultats de leurs prédécesseurs. Piqué au vif, la réaction anglaise est rapide, William Brouncker trouve un algorithme équivalent à celui de Bhāskara II, Bernard Frénicle de Bessy propose une table contenant toutes les solutions pour les valeurs de n inférieures à 150, qui sera finalement perdue, John Wallis redécouvre les résultats de Brahmagupta et les démontre rigoureusement. Frenicle de Bessy défie Brouncker avec la valeur n égal à 313, il reçoit en réponse non seulement la solution mais l'affirmation que son auteur n'a pas eu besoin de plus d'une heure ou deux pour trouver.

Les deux questions théoriques sous-jacentes, à savoir si pour toute valeur de n strictement positive et sans facteur carré il existe une solution et si la solution trouvée génère bien toutes les autres est finalement résolue par Joseph Louis Lagrange en 1767.