Modèles compartimentaux en épidémiologie - Définition

Extensions

Hétérogénéité des populations réelles

Sauf prise en compte explicite dans des classes, tous les individus ont le même nombre de contacts. Ceci peut se représenter par un graphe, où les individus sont des sommets (ronds) et sont liés s'ils sont en contact (traits). Dans la Figure (a), les individus ont tous 3 contacts. Appliquer un taux fixe d'infection repose sur le fait qu'en moyenne tout individu susceptible est en contact avec le même nombre d'individus infectieux. Dans la Figure (b), le nombre de contacts des individus est différent et trois (entourés en gris) jouent un rôle plus important dans la diffusion potentielle de l'épidémie.

Dans les modèles compartimentaux, la seule particularité d'un individu est la classe épidémiologique à laquelle il appartient. Ceci peut permettre de distinguer les individus en établissant des classes pour différents comportements : par exemple, dans des maladies sexuelles telles que le SIDA, il peut exister une classe pour les individus ayant un comportement à risque élevé (forte fréquence de rapports sexuels, rapports non protégés...) et une autre pour les individus ayant un comportement moins risqué. En créant de telles classes, les individus peuvent avoir des attributs prenant un petit nombre de valeurs : le comportement est ainsi un attribut, et risque élevé ou risque normal constituent ses deux valeurs. La population dans les modèles compartimentaux est ainsi hétérogène, c'est-à-dire que tous les individus ne sont pas absolument identiques. Autrement dit, les individus ne sont identiques que pour les attributs n'étant pas explicitement représentés dans une classe.

Les recherches du début des années 2000 à 2010 ont mis en avant le fait que les individus étaient très différents dans leur nombre de contacts. Certains individus peuvent ainsi avoir une poignée d'amis, ce qui limite leur exposition à des maladies infectieuses, tandis que d'autres peuvent être extrêmement sociaux, ce qui augmente la probabilité qu'ils soient infectés. Deux exemples de ces différences entre individus sont données par Bansal, Grenfell et Meyers. Premièrement, en 2003, deux voyageurs développèrent une pneumonie atypique, et l'un engendra 200 cas à Toronto tandis qu'aucun ne fut reporté pour l'autre à Vancouver. Deuxièmement, 60% des infections lors de l'épidémie de Gonorrhée de 1984 aux États-Unis provenaient de 2% de la population. Bien qu'il soit possible de prendre en compte le nombre de contacts des individus en utilisant des classes, cette approche est inadaptée. En effet, les classes ne permettent pas d'analyser la structure de la population et ses conséquences pour les maladies : il est possible de dire qu'un individu a plus de contacts qu'un autre, mais il est par exemple impossible de déterminer quels individus vacciner en priorité selon le rôle qu'ils jouent dans la population. Dans un cas simplifié, la population pourrait être constituée de deux communautés ne se côtoyant que par le biais d'un individu, et vacciner cet individu empêcherait la maladie de se répandre d'une communauté à l'autre.

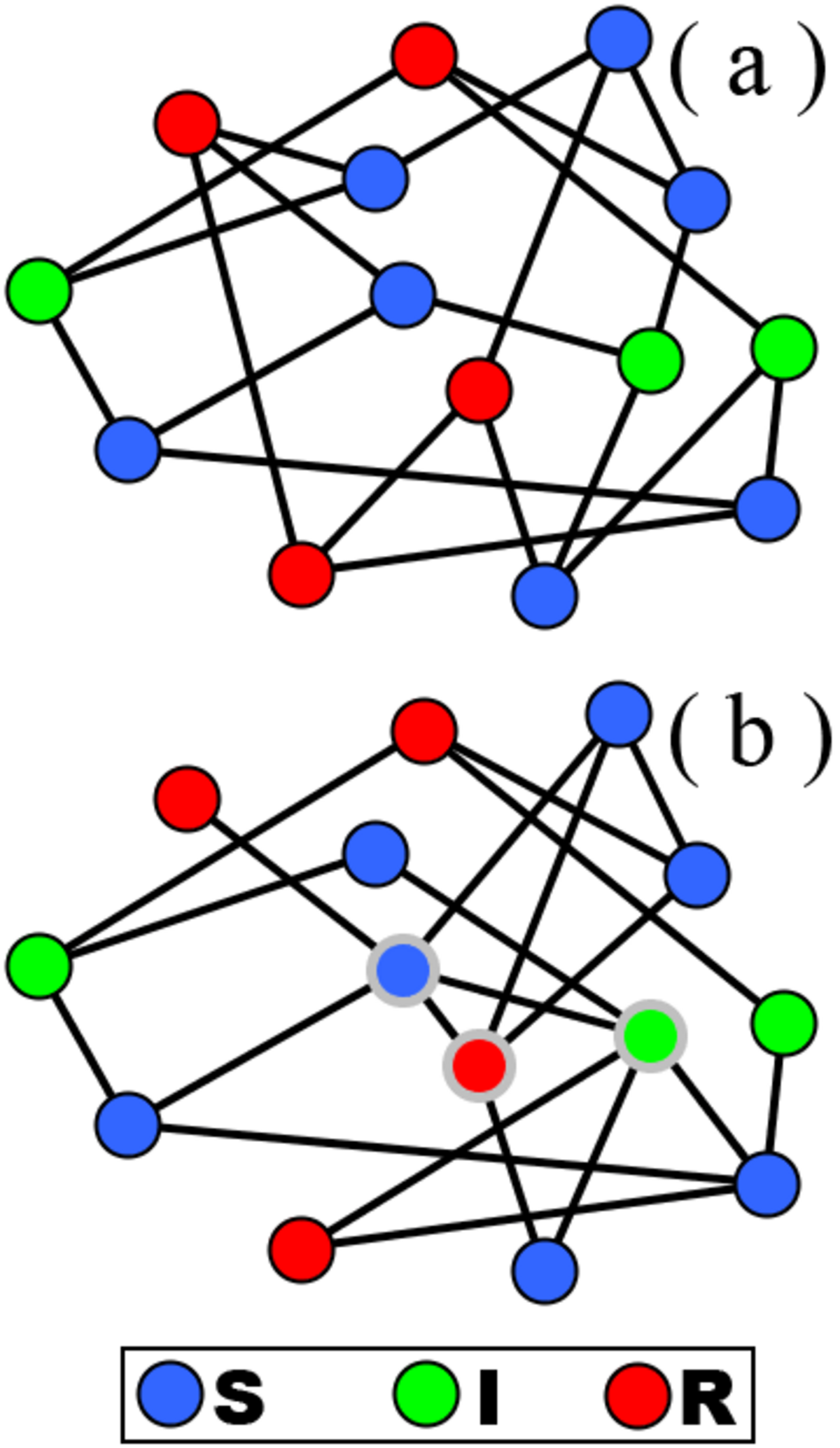
Prendre en compte le fait que les individus ont différents nombres de contact peut être réalisé sans avoir besoin de représenter explicitement les contacts par un graphe tel qu'illustré ci-contre. Parmi les approches, celle de Pastor-Satorras and Vespignani est une des plus citées et consiste à modifier les équations différentielles pour y inclure les différences en nombre de contacts. Les auteurs s'intéressent à un modèle SIS, c'est-à-dire que les individus sont susceptibles, peuvent devenir infectés et redeviennent susceptibles lors de la guérison ; il n'y a donc pas de décès ou d'immunité acquise. La proportion d'individus infectés au temps t est dénotée par ρ(t), le taux d'infection est dénoté par λ, et le nombre moyen de contacts par personne est dénoté < k > . Pour simplifier le modèle, la quantité d'individus guéris n'est pas spécifiée par un taux : l'unité de temps est considérée comme étant choisie assez longue pour que tous les individus soient guéris d'une étape à une autre. Ainsi, si tous les individus avaient le même nombre de contacts, alors l'évolution de la proportion d'individus infectés serait donnée par la dérivée :

La partie − ρ(t) résulte de la rémission de tous les individus infectés. La seconde moitié se comprend de la façon suivante : chacun des ρ(t) individus a < k > contacts, chacun de ces contacts est un individu sain avec probabilité 1 − ρ(t), et l'infection d'un individu sain en contact est faite avec un taux λ. Dans le cas où les individus n'ont pas tous le même nombre de contacts, l'équation s'intéressera alors au taux d'individus infectés ayant k contacts, ce qui est dénoté par ρ_k(t).

La méthode de Pastor-Satorras et Vespignani est particulièrement connue en raison de son résultat : le calcul du taux de reproduction de base donne R₀ = 0 lorsque ρ_k(t) = e^c.x ^{− α}, où c et α sont deux constantes. De façon simplifié, ce résultat établit que dans une population où la majorité des individus a peu de contacts et quelques uns en ont beaucoup, ce qui est souvent le cas, alors il n'existe pas de seuil à la propagation de la maladie : il est impossible d'empêcher la maladie de se propager. Cependant, le résultat a été excessivement repris dans cette forme simplifiée sans tenir compte des hypothèses sur lesquels il repose. En effet, Pastor-Satorras et Vespignani considèrent que seule la propriété ρ_k(t) = e^c.x ^{− α} est en place et qu'en tous autres aspects la population est aléatoire ; de plus, l'exposant est choisi et la population est considérée de taille infinie. Des études récentes ont montré que toutes les hypothèses doivent être simultanément vérifiées pour parvenir au résultat. Par exemple, il suffit de considérer un modèle compartimental autre que SIS ou une population avec davantage de propriétés pour trouver de nouveau des conditions dans lesquelles la maladie ne peut plus se propager.

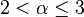
Déplacements

Le modèle de Bartlett considère que les individus au sein de deux villes (bleu et jaune) sont sains ou infectés. Les individus peuvent se déplacer entre les villes et interagissent.

La population réelle est répartie dans plusieurs villes. À l'intérieur d'une ville, les individus peuvent se contaminer. Un individu contaminé peut se déplacer dans une autre ville et y propager la maladie, et d'une façon similaire un individu sain peut se déplacer dans une ville où il sera infecté et ramener la maladie dans sa ville d'origine. Modéliser ces aspects permet de prendre en compte l'évolution de la maladie dans un espace. Le modèle de Bartlett est cité par Arino comme le premier à avoir pris en compte l'aspect spatial. Les individus sont dans deux états possibles, S et I. Deux endroits sont définis : les individus se trouvant au premier peuvent être dans les états S₁ et I₁, tandis que les individus se trouvant au second peuvent être dans les états S₂ ou I₂. Afin d'autoriser les déplacements de population, il est possible pour un individu de changer d'état entre S₁ et S₂ d'une part, et entre I₁ et I₂ d'autre part. Le modèle de Bartlett ne se limite pas au strict déplacement d'individus entre les deux endroits puisqu'il considère que les individus dans deux villes interagissent : par exemple, la proportion d'individus de S₁ devenant infectée n'est pas simplement β₁I₁ mais β₁I₁ + β₂I₂, ce qui représente l'hypothèse que tous les individus dans S₁ sont en contact avec un même nombre d'individus dans I₁ et I₂.

Rebecca Grais et ses collègues de l'Université Johns-Hopkins ont utilisé une approche compartimentale pour décrire la diffusion d'une maladie dans le cas où les passagers se déplaçaient par avion. Les passagers sains (jaune) et nouvellement infectés (bleu) se déplacent, tandis que ceux trop atteints restent confinés dans leur ville.

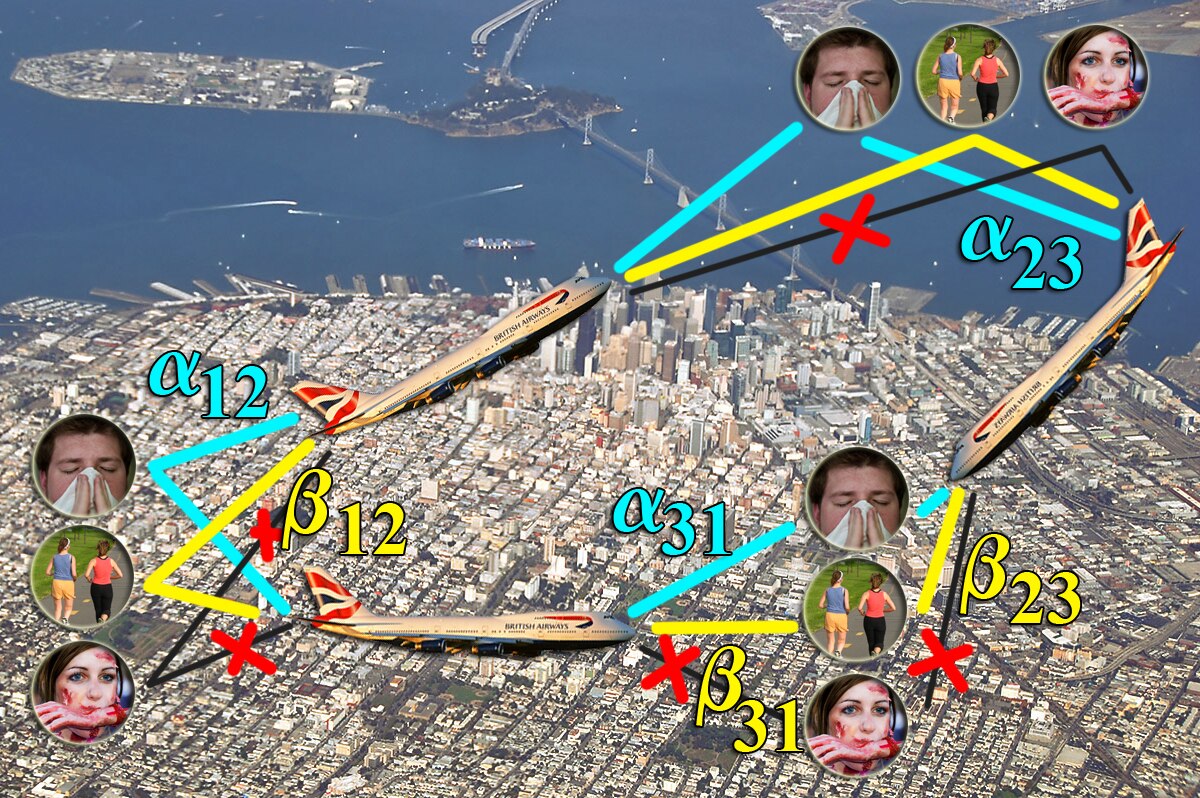
Le modèle de Grais, Ellis et Glass s'intéresse à la diffusion de la grippe lorsque les individus voyagent par avion entre des villes. Les auteurs considèrent les individus d'une ville i comme pouvant être susceptibles, dans la période d'incubation (c'est-à-dire qu'ils ont été infectés mais ne le savent pas encore car la maladie ne s'est pas déclarée) ou infectieux. L'hypothèse est que les individus, ou les compagnies aériennes, appliquent un principe de précaution : les individus infectieux ne voyagent pas, tandis que les autres y sont autorisés. Ainsi, comme dans la réalité, la maladie peut être véhiculée par des individus en période d'incubation. Afin d'être réaliste, le modèle calcule le nombre d'individus prenant des vols à partir du nombre d'habitants dans des grandes villes mondiales. La zone des villes et le mois sont également utilisés pour prendre en compte les variations saisonnières de la grippe. En considérant un ensemble de villes entre lesquelles les individus dans certains états peuvent se déplacer, ce modèle montre la nécessité d'une modélisation sous forme de multi-graphe. Concrètement, un multi-graphe décrit les lieux par des sommets, et deux lieux peuvent être reliés par autant d'arcs qu'il y a d'états permettant de s'y rendre. Par exemple, si les individus sains et en période d'incubation peuvent se rendre de Paris à Manille, alors Paris et Manille sont représentés par deux sommets, et il existe deux arcs allant de Paris à Manille : le premier représente le flot de passagers sains, et le second le flot de passagers en période d'incubation.

Les travaux de Fromont, Pontier et Langlais cités par Arino s'intéressent à une maladie se transmettant entre les chats : ainsi qu'ils le notent, « les structures sociales et spatiales des chats changent selon la densité », qui va de 1 jusqu'à 2000 chats par km². Les auteurs considèrent les chats dans deux types de lieux : les « fermes » et les « villages ». Dans les fermes, il y a peu de chats et tous se rencontrent donc, tandis que dans un village le nombre de chats est trop élevé pour qu'ils soient tous en contact. Ainsi, la maladie fonctionne différemment selon le lieu considéré, ce qui est rarement appliqué à des modèles avec déplacement. Arino suggère que conjuguer le déplacement avec l'hétérogénéité de la population constitue une piste pour des recherches futures.

Prise en compte de l'âge

Nombre estimés d'individus diagnostiqués avec le SIDA par âge lors du diagnostic.

La distribution de la population par âge peut être obtenue de statistiques nationales ou internationales, telles celles fournies par l'Organisation des Nations Unies.

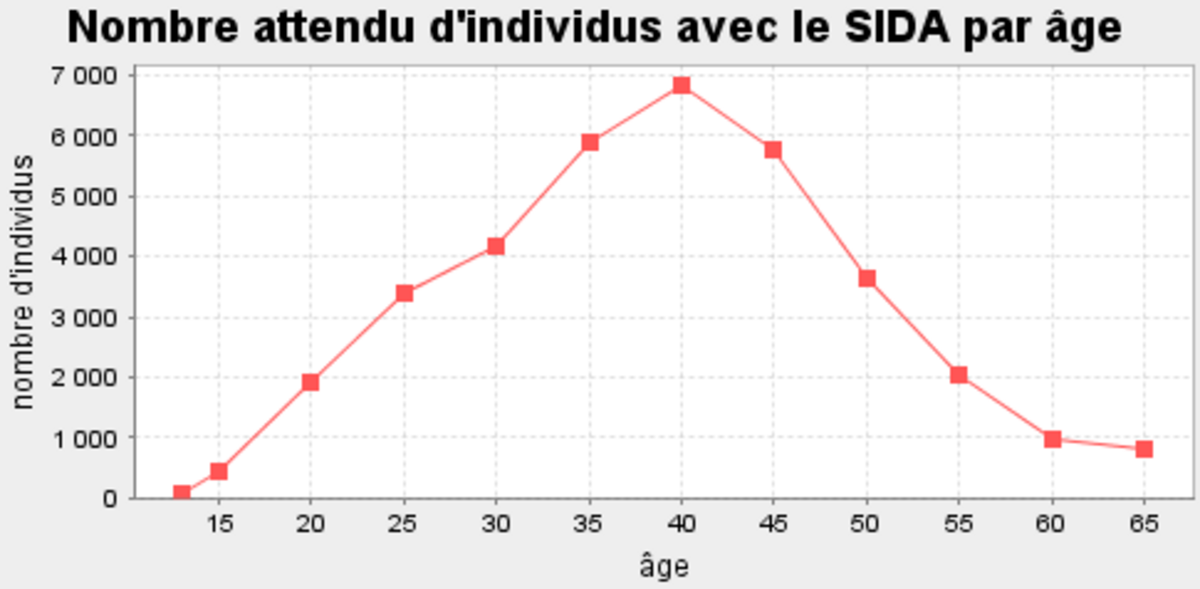
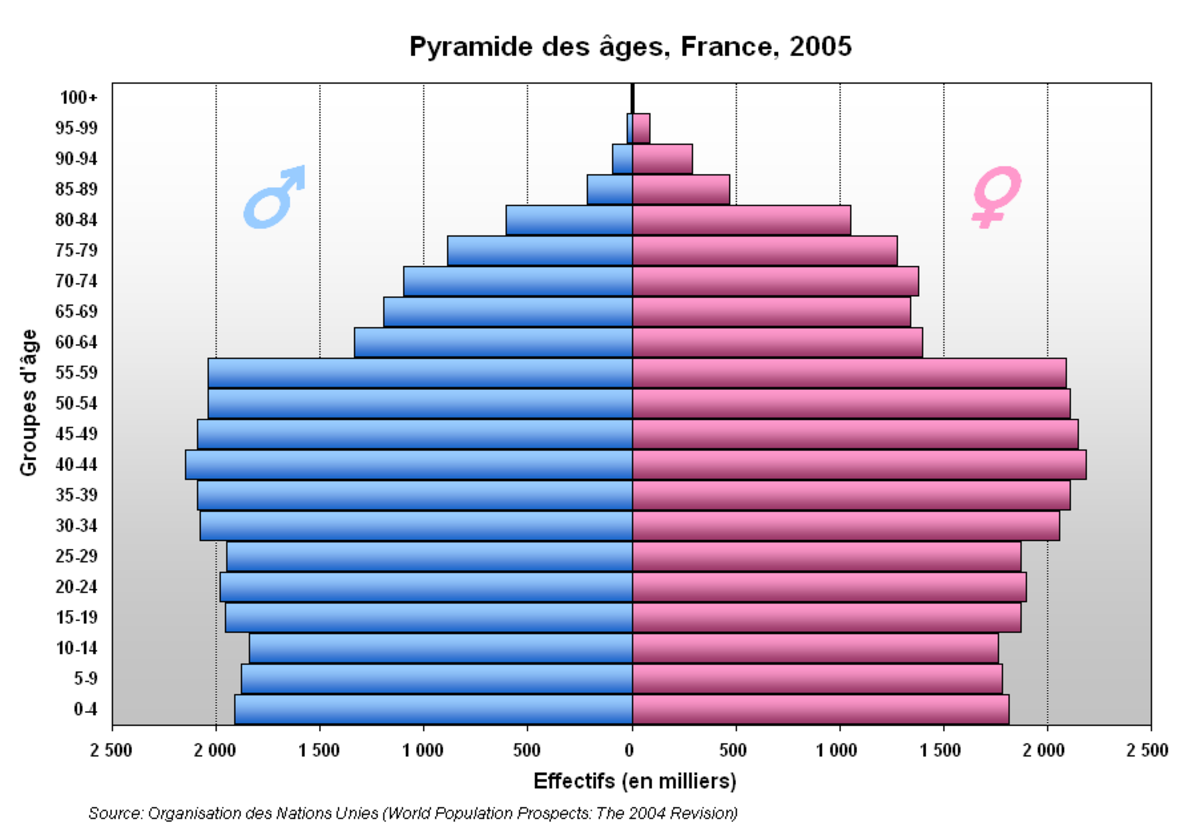
L'âge peut être un facteur important de la diffusion d'une maladie pour deux raisons. Premièrement, la résistance des sujets peut dépendre de l'âge. Un exemple extrême consiste à séparer les enfants des adultes : dans le cas de d'épidémies de rougeole aux États-Unis en 1827 et 1828, la population étudiée était composée à 21% d'enfants mais ceux-ci représentaient 44% des décès. Deuxièmement, le comportement des sujets change avec l'âge : ainsi, il est considéré que la probabilité qu'un individu s'engage dans une activité sexuelle à risque décroît avec l'âge, et des modèles prennent en compte l'impact de l'âge sur des aspects tels que le taux de changements de partenaires sexuels. La prise en compte de l'âge se fait en utilisant une nouvelle variable a. Ainsi, dans le modèle SIR, les quantités d'individus infectés au temps t ne sont plus seulement dénotées S(t), I(t) et R(t), mais S(t,a), I(t,a) et R(t,a) pour représenter la quantité avec un âge donné. Au temps t, p(t,a)S(t,a) individus avec l'âge a deviennent infectés. Si ces individus ont des contacts uniquement avec des individus du même âge a, alors la force de l'infection ne dépend que du nombre de personnes infectées d'âge a et du taux d'infection pour cet âge :

En revanche, si un individu a des contacts avec des individus de tout âge, alors il faut prendre en compte le taux κ(a,x) avec lequel des individus sains d'âge a sont en contact avec des individus infectés d'âge x. Ainsi, la force avec laquelle les individus d'âge a seront infectés consiste à considérer le nombre de personnes pour chaque âge x possible et le taux d'infection associé à cet âge. La population étant considérée comme continue par rapport à l'âge, cette approche s'exprime par:

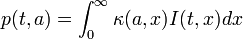
Dans la version du modèle SIR sans prise en compte de l'âge, l'évolution du nombre d'individus infectés était donnée par dI(t) / dt = p.S(t).I(t) − α.I(t). Dans le cas avec âge, p est fonction de t et a. Dans son expression ci-dessus, p(t,a) dépend de l'intégrale de I(t,x). Ainsi, le changement du nombre d'individus infectieux, c'est-à-dire la dérivée de I(t,x), dépend de l'intégrale de I(t,x) pour la partie pS(t)I(t), et de I(t,x) (pour la partie − αI(t). L'équation devient donc intégro-différentielle, puisqu'elle fait intervenir à la fois l'intégrale et la dérivée de la fonction.

Parmi les modèles compartimentaux avec prise en compte de l'âge, Sido Mylius et ses collègues de l'Institut Nationale de Santé Publique et Environnement (RIVM, Pays-Bas) se sont intéressés à un modèle SEIR pour la grippe. La distribution des âges dans leur modèle provient des statistiques des Pays-Bas, et la transmission entre individus de deux groupes d'âge provient de l'étude sur la transmission des maladies respiratoires infectieuses de Wallinga, Teunis et Kretzschmar, elle même fondée sur la fréquence des contacts entre individus de deux classes d'âge à Utrecht en 1986. La fréquence de contacts entre individus de deux classes d'âges est traditionnellement exprimée par la matrice WAIFW (who acquires infection from whom, soit « qui acquiert une infection de qui »). Cette matrice est nécessairement non-symétrique : par exemple, tout enfant a un parent (c'est-à-dire adulte) avec qui il est en contact, mais tout adulte n'a pas nécessairement un enfant, et ainsi la fréquence des contacts d'un enfant vers un adulte est en moyenne plus élevée que d'un adulte vers un enfant. Dans le modèle de Mylius, les individus pour chaque état sont divisés par âge, puis par groupe de risque. Le nombre de nouvelles infections pour des individus sains d'âge a et groupe r est calculé en considérant le nombre d'individus sains S_a,r, la fréquence c_a,a' de leurs contacts avec des individus d'âge a' (considérée comme dépendant seulement de l'âge), le nombre I_a',r' d'individus infectieux avec lesquels ils peuvent être en contact, et la probabilité q de transmettre la maladie lors d'un contact. Dans ce modèle, la population est considérée comme discrète, et l'évolution du nombre d'individus sains fait ainsi intervenir une somme plutôt qu'une intégrale :

Population proactive : agir face à la maladie

Lors de la diffusion de la grippe A (H1N1), une large campagne de vaccination a été organisée. Les médias montrent ainsi des responsables se faire vacciner, tel le président des États-Unis, Barack Obama, en décembre 2009.

Comme « beaucoup de modèles de transmission des maladies », les modèles exposés dans les sections précédentes « considèrent une population passive qui ne répondra pas (changera son comportement) face à la diffusion d'une maladie infectieuse ». Cependant, il existe des campagnes pour sensibiliser la population, comme la Journée mondiale de lutte contre le SIDA, ou pour inciter à la vaccination. Des campagnes de masse peuvent déboucher sur des résultats très faibles, tels que la prise d'un test par moins de 1% du public concerné. Ainsi, l'étude de la façon dont la population réagit face à l'information fait partie de certains modèles épidémiologiques.