Modèles compartimentaux en épidémiologie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les modèles mathématiques de maladies infectieuses, d'abord outils purement théoriques, ont commencé à être mis en pratique avec le problème du SIDA dans les années 1980. La course d'une épidémie dans une population dépendant de paramètres extrêmement nombreux (stades cliniques possibles, déplacement des individus, souches de la maladie), les modèles mathématiques se sont progressivement affirmés comme outils d'aide à la décision pour les politiques publiques. En effet, les modèles permettent de prévoir les conséquences pour la population d'actions aussi variées que la vaccination, la mise en quarantaine ou la distribution de tests de dépistage. Une approche fondatrice dans les années 1920 fut celle des modèles compartimentaux, qui divisent la population en classes épidémiologiques tels que les individus susceptibles d'être infectés, ceux qui sont infectieux, et ceux qui ont acquis une immunité suite à la guérison. Depuis, cette approche fut utilisée pour modéliser de très nombreuses maladies, et continue d'être un sujet de recherche actif en prenant en compte de nouveaux éléments tels que les découvertes de la science des réseaux.
Principes fondamentaux
Compartiments et règles
Un modèle épidémiologie est formé de deux parties : compartiments et règles. Les compartiments divisent la population dans les différents états possibles par rapport à la maladie. Par exemple, William Ogilvy Kermack et Anderson Gray McKendrick proposèrent un modèle fondateur dans lequel la population était divisée en individus susceptibles de contracter la maladie (compartiment S), et en individus infectieux (compartiment I). Les règles spécifient la proportion des individus passant d'une classe à une autre. Ainsi, dans un cas à deux compartiments, il existe une proportion p(S → I) d'individus sains devenant infectés et, selon les maladies, il peut aussi exister une proportion p(I → S) d'individus infectieux étant guéris. L'acronyme utilisé pour un modèle est généralement fondé sur l'ordre de ses règles. Dans le modèle SIS, un individu est initialement sain (S), peut devenir infecté (I) puis être guéri (S); si la guérison n'était pas possible, alors il s'agirait d'un modèle SI.
Sept compartiments sont couramment utilisés : S, I, E, D, R, M et C. Le compartiment S est nécessaire, puisqu'il doit initialement exister des individus n'ayant pas encore été infectés. Lorsqu'un individu du compartiment S est exposé à la maladie, il ne devient pas nécessairement capable de la transmettre immédiatement, selon l'échelle de temps considérée dans le modèle. Par exemple, si la maladie nécessite deux semaines pour rendre l'individu infectieux (ce qui est appelé une période de latence de deux semaines) et que le modèle représente l'évolution journalière de la population, alors l'individu ne va pas directement dans le compartiment I (infectieux) mais doit passer par un compartiment intermédiaire. Un tel compartiment est dénoté E, pour les individus exposés.
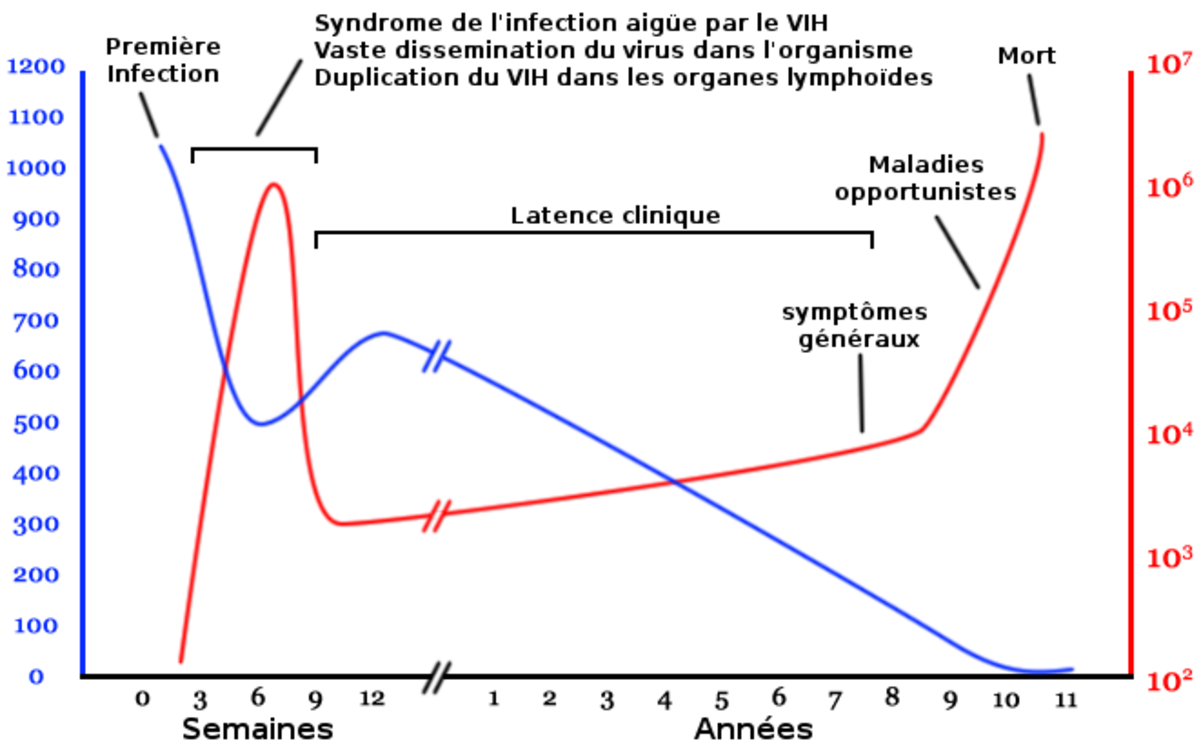
Selon les maladies, il peut être utile de distinguer les individus infectés. Si la maladie est causée par des organismes parasites tel le ver parasite ou les tiques, alors la concentration de ces organismes peut justifier de diviser la classe I en plusieurs classes représentant plusieurs niveaux de concentration. Lorsque la maladie est causée par des virus ou des bactéries, un grand nombre de modèles ne divisent pas la classe I : ils considèrent que l'individu est infecté ou ne l'est pas. Cependant, dans le cas d'un virus, il existe un analogue à la concentration en organismes parasitaires : il s'agit de la charge virale, qui exprime la concentration du virus dans un volume donné tel que le sang. Les individus peuvent donc être distingués selon leur charge, puisque celle-ci les rend infectieux à des niveaux différents, ainsi qu'illustré ci-contre dans le cas du VIH.
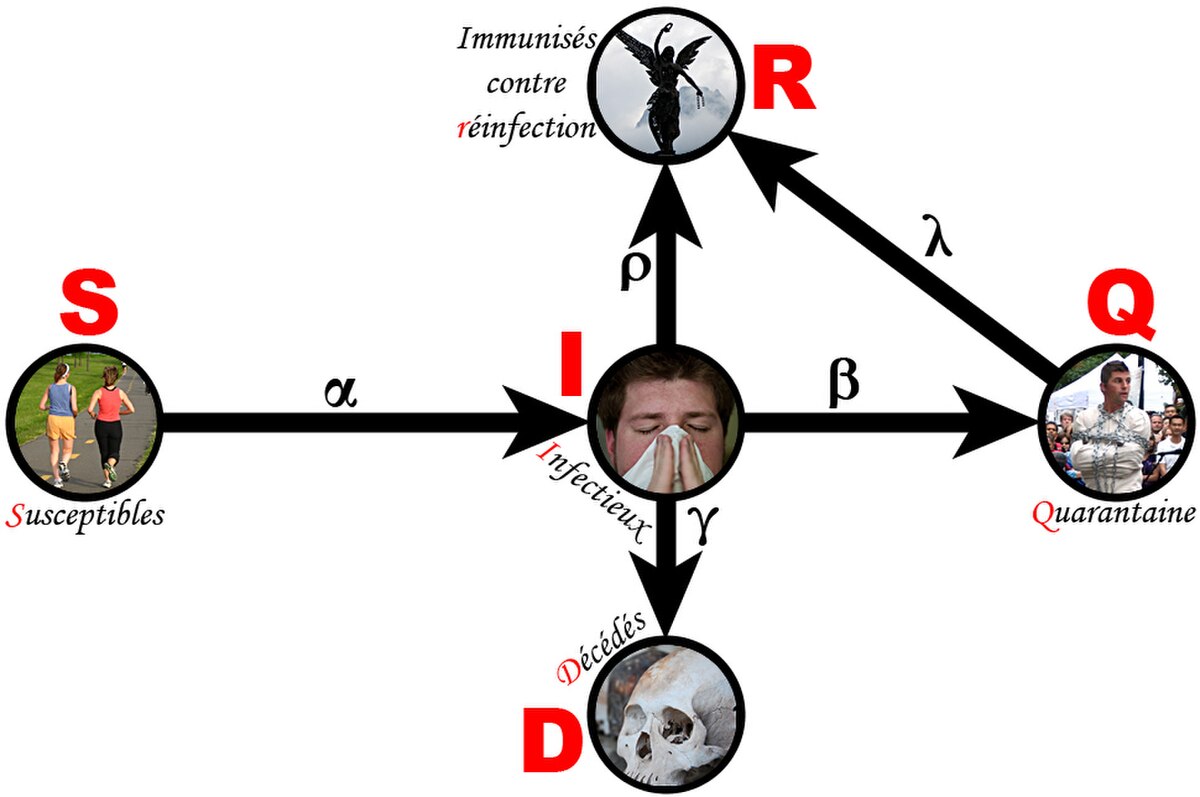
Après qu'un individu ait été infecté, trois cas de figure peuvent se produire. Premièrement, l'individu peut décéder, auquel cas il relève du compartiment D. Deuxièmement, la maladie peut se terminer d'elle-même et conférer à l'individu une immunisation contre la réinfection, et il est assigné à un compartiment R. Enfin, l'individu peut toujours être infectieux mais il se retrouve isolé de la population par politique de quarantaine, correspond à un compartiment Q. Séparer les individus morts des individus en quarantaine permet également de prendre en compte que ces derniers peuvent éventuellement guérir et revenir au compartiment S. Parmi les autres compartiments possibles, M représente les individus disposant d'une immunité à la naissance (par voie maternelle), et C représente les individus porteurs de la maladie (carriers) mais qui n'en expriment pas les symptômes.
Représentation mathématique à l'aide d'équations différentielles
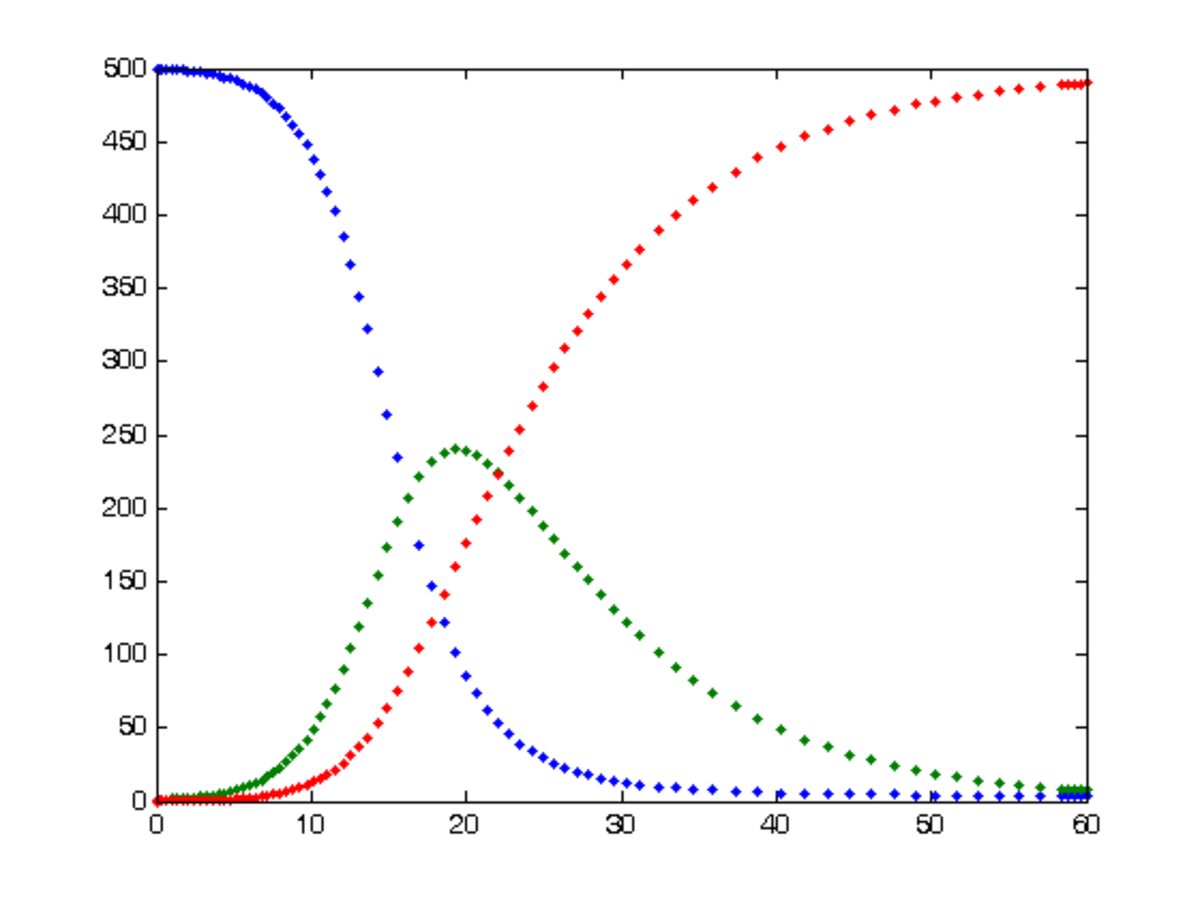
Les modèles compartimentaux permettent d'estimer comment le nombre d'individus dans chaque compartiment varie au cours du temps. Par abus de notation, la lettre utilisée pour représenter un compartiment est également employée pour représenter le nombre d'individus dans le compartiment. Par exemple, S est utilisé dans une équation pour représenter le nombre d'individus sains. Une formulation plus rigoureuse, et parfois employée, consiste à utiliser S(t) à la place de S, ce qui explicite qu'il s'agit d'une fonction et que le nombre dépend du temps t. Pour savoir comment le nombre d'individus dans un compartiment varie au court du temps, il est nécessaire de savoir comment déduire le nombre d'individus d'une étape à une autre, c'est-à-dire du temps t au temps t + 1. Cette différence dans le nombre d'individus est donnée par la dérivée. Ainsi, dS / dt correspond à la balance du nombre d'individus par rapport au compartiment S. Une balance négative signifie que des individus sortent, tandis qu'une balance positive signifie que des individus entrent. La balance dI / dt porte le nom d’incidence car elle représente le nombre d'infections de la maladie.
Dans le cas d'un modèle SIR, un individu commence sain, peut devenir infecté puis se remettre de sa maladie avec une immunisation. Si le taux d'infection (aussi appelé force de l'infection) est dénoté par p, alors dS / dt = − p.S.I. Ceci exprime qu'un individu infectieux infecte en moyenne p individus sains, et ces individus nouvellement infectés sont supprimés du compartiment S. L'équation mettant en relation la fonction S et sa dérivée, il s'agit d'une équation différentielle. Dans les modèles simples, ces équations sont des équations différentielles ordinaires (EDO, ou ODE en anglais). Si la proportion d'individus infectieux retirés de la population est α, alors dI / dt = p.S.I − α.I, ce qui signifie que le nombre d'individus infectieux augmente avec ceux nouvellement infectés et diminue avec ceux retirés. Enfin, tous les individus guéris sont d'anciens individus infectieux, d'où dR / dt = α.I. En additionnant les trois équations différentielles, il apparaît que dS / dt + dI / dt + dR / dt = 0, ce qui signifie que le nombre d'individus dans la population est toujours le même. Ce modèle considère donc une population stable (ou close), c'est-à-dire dans laquelle il n'y a ni naissance, ni émigration ou immigration. L'hypothèse d'une population stable est justifiée lorsque l'épidémie se déroule sur une petite échelle de temps, et si ce n'est pas le cas alors il peut devenir important de considérer les effets démographiques. Dans le cadre d'un modèle avec un état intermédiaire comme SEIR, les équations pour dS/dt et dR/dt sont les mêmes. En dénotant par β le taux d'individu exposés qui deviennent infectieux, alors dE / dt = p.S.I − β.I, et dI / dt = β.E − α.I.
L'épidémie de peste bubonique à Eyam, en Angleterre, entre 1665 et 1666, constitue un exemple célèbre illustrant la dynamique d'un modèle SIR dans un cas réel. Devant la peste, le prêtre William Mompesson proposa des mesures de quarantaine qui furent suivirent par la population, afin d'empêcher que la maladie ne se diffuse à d'autres communautés. Ceci s'avéra être une erreur. En effet, la maladie était principalement transmise par les puces qui ne se tournaient vers l'homme que lorsqu'elles ne trouvaient plus de rats. La politique de quarantaine garde les puces, les rats et les hommes en contacts ce qui augmenta drastiquement le taux d'infection ; de plus, elle n'empêche pas les rats de se répandre à d'autres communautés. Cette politique entraîna le décès de 76% des habitants. Les quantités d'individus sains (S) et infectés (I) furent écrites pour plusieurs dates, et la quantité d'individus supprimés (R) peut être déduite connaissant la population de départ. En calibrant sur ces données, un modèle SIR donne p = 2.73 et α = 0.0178. Sur cet épisode, Brauer conclut : « le message que cela suggère aux mathématiciens est que les stratégies de contrôle fondées sur des modèles erronés peuvent être dangereuses, et qu'il est essentiel de distinguer entre les hypothèses qui simplifient mais ne changent pas substantiellement les effets prédits, et les hypothèses erronées qui font une différence importante ».
Taux de reproduction de base
| Maladie | Mode de transmission | R0 |
|---|---|---|
| Rougeole | Dans l'air | 12–18 |
| Coqueluche | Dans l'air | 12–17 |
| Diphtérie | Salive | 6–7 |
| Variole | Contact physique | 5–7 |
| Polio | Ingestion de matière fécale | 5–7 |
| Rubéole | Dans l'air | 5–7 |
| Oreillons | Dans l'air | 4–7 |
| VIH/SIDA | Contact sexuel | 2–5 |
| Pneumonie atypique | Dans l'air | 2–5 |
| Grippe | Dans l'air | 2–3 |
Étant donné une maladie, une question fondamentale est de savoir si elle peut se propager dans la population. Ceci revient à calculer le nombre moyen d'individus qu'une personne infectieuse pourra infecter, tant qu'elle sera contagieuse. Ce nombre est appelée le taux de reproduction de base, et est dénotée R0. Elle est considérée dans une population où tous les individus sont sains, sauf l'individu infectieux introduit. Si R0 < 1, alors un individu en infecte en moyenne moins d'un autre, ce qui signifie que la maladie disparaîtra de la population. À l'opposé, si R0 > 1, alors la maladie peut se propager dans la population. Déterminer R0 en fonction des paramètres du modèle permet ainsi de calculer les conditions dans lesquelles la maladie se propage.
Comme le notent van den Driessche et Watmough, « dans le cas d'un seul compartiment infecté, R0 est simplement le produit du taux d'infection et de sa durée moyenne ». Lorsque le modèle est simple, il est souvent possible de trouver une expression exacte de R0. Pour cela, une technique couramment employée consiste à considérer que la population est à l'état d'équilibre. Autrement dit, le nombre d'individus dans chaque compartiment ne varie plus. Dans le cas du modèle SI, cela revient à poser les conditions dS / dt = 0 et dI / dt = 0. Pour résoudre un tel système d'équations différentielles, c'est-à-dire pour trouver les points d'équilibre, une possibilité est d'utiliser l'analyse qualitative.
Lorsqu'il existe plusieurs compartiments représentant des individus infectieux, d'autres méthodes sont nécessaires, telle la méthode next-generation matrix (« matrice de la génération suivante ») introduite par Diekmann. Dans l'approche de van den Driessche et Watmough à cette méthode, la population est divisée en n compartiments x1,...,xn dont les m premiers représentent les individus infectés. Autrement dit, au lieu de s'intéresser à un seul compartiment d'individus infectés comme précédemment, la méthode considère que les individus infectés sont distribués sur m compartiments. Le but est donc de voir s'établir les taux d'évolution de la population dans chacun de ces compartiments.
Pour cela, il faut prendre deux aspects en compte. Premièrement, des individus peuvent avoir été nouvellement infectés, et proviennent ainsi de compartiments autre que les m premiers. Deuxièmement, les individus infectés peuvent se déplacer entre les compartiments infectés. Formellement, le taux d'individus nouvellement infectés rejoignant le compartiment i est dénoté Fi(x). La différence entre les taux d'individus sortant et entrant dans le compartiment i par d'autres moyens que l'infection est notée Vi(x). Déterminer l'évolution d'un compartiment dépend de tous les autres compartiments, ce qui conduit à l'expression du système par deux matrices carrées F et V de taille
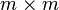
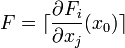
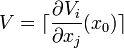
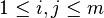
La matrice de génération suivante est M = FV − 1. Une propriété de cette matrice est que si sa plus grande valeur-propre est supérieure à 1, alors les générations grandissent en taille; à l'opposé, si la plus grande valeur propre est inférieure à 1, alors les générations diminuent. La plus grande valeur propre correspond donc au taux de reproduction de base. La plus grande valeur propre d'une matrice A est connue comme son rayon spectral et noté ρ(A). Ainsi, R0 = ρ(M).
L'approche matricielle pour calculer le taux de reproduction de base dans des modèles complexes montre le lien qui existe entre les modèles compartimentaux et les modèles matriciels de population.